Question

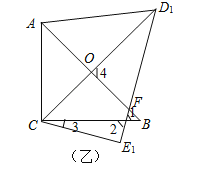
【题目】把一副三角板如图放置 其中∠ACB=∠DEC=90，∠A=45，∠D=30，斜边 AB=4，CD=5，把三角板DCE绕点C顺时针旋转15得到三角形D1CE (如图二)，此时AB与CD1交于点O，则线段AD1的长度为( )

A. B. C. D. 4

Answer 1

【答案】A

【解析】解：如图乙所示，∵∠3=15°，∠D1CE1=90°-30°=60°，∴∠BCO=60°-15°=45°．又∵∠ACB=90°，∴∠ACO=45°，∴∠AOC=∠AOD1=90°．∵∠B=∠CAO=45°，∴AO=OB=OC=

AB=2（cm）．∵∠ACB=90°，∴CO=AB=×4=2（cm）．又∵CD1=5（cm），∴OD1=CD1﹣OC=5﹣2=3（cm）．在Rt△AD1O中，AD1===（cm）．故选A．