题目内容
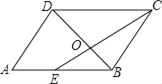
【题目】如图，平行四边形ABCD中，E是AB的中点，CE和BD交于点O，如△ODC的面积为4，则四边形AEOD的面积是（ ）
A. 3 B. 4 C. 5 D. 6
【答案】C
【解析】
根据平行四边形的性质可得出CD∥BE、CD=AB，进而可得出△COD∽△EOB，根据相似三角形的性质可求出S△EOB和
的值，由三角形的面积可得出S△BCD=
S△COD=6，再根据平行四边形的性质结合S四边形AEOD=S△ABD-S△EOB，即可求出四边形AEOD的面积．
解：∵四边形ABCD为平行四边形，
∴CD∥BE，CD=AB，
∴△COD∽△EOB，
∴
=（
）2．
∵E是AB的中点，
∴AB=2BE，
∴CD=2BE，
∴
=22=4，=2，
∴S△EOB=1，BD=BO+OD=OD，
∴S△BCD=S△COD=6．
∵四边形ABCD为平行四边形，
∴S△ABD=S△BCD=6，
∴S四边形AEOD=S△ABD-S△EOB=6-1=5．
故选：C．
练习册系列答案
名牌学校分层周周测系列答案
黄冈海淀全程培优测试卷系列答案
相关题目
