题目内容
【题目】(1)阅读理解
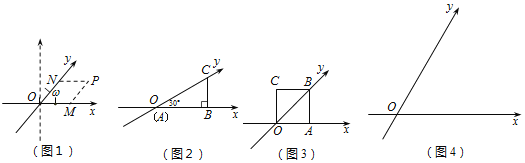
我们知道,平面内互相垂直且有公共原点的两条数轴构成平面直角坐标系.如果两条数轴不垂直,而是相交成任意的角ω(0°<ω<180°且ω≠90°),那么这两条数轴构成的是平面斜坐标系.如图1,经过平面内一点P作坐标轴的平行线PM和PN交x轴和y轴于M、N,点M、N在x轴和y轴上所对应的数分别叫做P点的x坐标和y坐标.
如图2,ω=30°,直角三角形的顶点A在坐标原点O,点B、C分别在x轴和y轴上,AB=![]() ,则点B、C在此斜坐标系内的坐标分别为B ,C .
,则点B、C在此斜坐标系内的坐标分别为B ,C .
(2)尝试应用
如图3,ω=45°,O为坐标原点,边长为1的正方形OABC一边OA在x轴上,设点G(x,y)在经过A、C两点的直线上,求y与x之间满足的关系式.
(3)深入探究
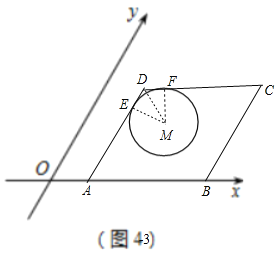
如图4,ω=60°,O为坐标原点,M(2,2),圆M的半径为![]() .有一个内角为60°的菱形,菱形的一边在x轴上,另有两边所在直线恰好与圆M相切,求此菱形的边长.
.有一个内角为60°的菱形,菱形的一边在x轴上,另有两边所在直线恰好与圆M相切,求此菱形的边长.
【答案】(1)(![]() ,0),C(0,2); (2)y=-
,0),C(0,2); (2)y=-![]() x+
x+![]() .(3)1或2或3.
.(3)1或2或3.
【解析】
(1)根据平面斜坐标系中点的坐标的定义计算即可;
(2)求出A、C两点坐标,利用待定系数法即可解决问题;
(3)分三种情形①如图4-1中,当菱形ABCD的边AD、BC与⊙M相切于E、F时;②如图4-2中,当菱形ABCD的边AD、DC与⊙M相切于E、F时,连接EM、MF;③如图4-3中,当菱形ABCD的边AD、DC与⊙M相切于E、F时,连接EM、DM、MF.分别求解即可解决问题;
(1)如图2中,
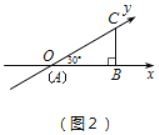
B(![]() ,0),C(0,2),
,0),C(0,2),
故答案为(![]() ,0),C(0,2);
,0),C(0,2);
(2)如图3中,由题意C(-1,![]() ),A(1,0),
),A(1,0),
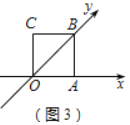
设直线AC是解析式为y=kx+b,
则有: ,
,
解得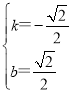
∴y=-![]() x+
x+![]() .
.
(3)①如图4-1中,当菱形ABCD的边AD、BC与⊙M相切于E、F时,作BH⊥AD于H.

∵四边形BHEF是矩形,
∴BH=EF=![]() ,
,
在Rt△ABH中,∵∠BAH=60°,
∴AB=BH÷cos60°=2.
②如图4-2中,当菱形ABCD的边AD、DC与⊙M相切于E、F时,连接EM、MF.
易知AE=![]() ,DE=
,DE=![]() ,所以AD=AE-DE=1,
,所以AD=AE-DE=1,
∴AB=AD=1.
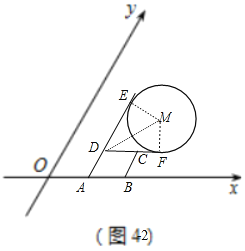
③如图4-3中,当菱形ABCD的边AD、DC与⊙M相切于E、F时,连接EM、DM、MF.
易知AE=![]() ,DE=
,DE=![]() ,所以AD=AB=AE+DE=3.
,所以AD=AB=AE+DE=3.
综上所述,菱形的边长为1或2或3.

 阅读快车系列答案
阅读快车系列答案