题目内容
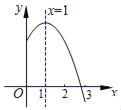
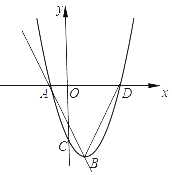
【题目】如图,已知抛物线y=x2+ax﹣3交x轴于点A,D两点,交y轴于点C,过点A的直线与x轴下方的抛物线交于点B,已知点A的坐标是(﹣1,0).
(1)求a的值;
(2)连结BD,求△ADB面积的最大值;
(3)当△ADB面积最大时,求点C到直线AB的距离.
【答案】(1)-2;(2)8;(3)![]()
【解析】
(1)点A(-1,0),代入二次函数表达式即可;
(2)当点B在抛物线顶点上时,△ABD的面积最大;
(3)求出直线AB的解析式为:y=-2x-2,过点C作CE⊥AB于E,证明△AOF∽△CEF,即可求解.
(1)∵点A(﹣1,0),
∴1﹣a﹣3=0,
∴a=﹣2;
(2)当点B在抛物线顶点上时,△ABD的面积最大,
∴B(1,﹣4),
∴S=![]() ×4×4=8;
×4×4=8;
(3)∵设直线AB的解析式为y=kx+b,
将点A(﹣1,0),B(1,﹣4)代入,得
![]() ,
,
![]() ,
,
∴直线AB的解析式为:y=﹣2x﹣2,
∴AO=1,OF=2,CF=1,
过点C作CE⊥AB于E,
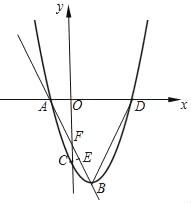
∴∠AOF=∠CEF=90°,∠AFO=∠CFE
∴△AOF∽△CEF
![]() ,
,
∴AF=![]() ,
,
∴![]() ;
;

练习册系列答案
 黄冈小状元解决问题天天练系列答案
黄冈小状元解决问题天天练系列答案
相关题目