题目内容
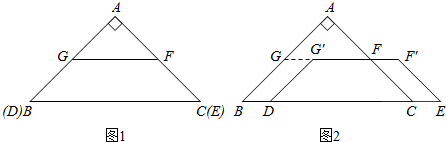
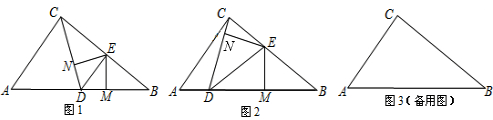
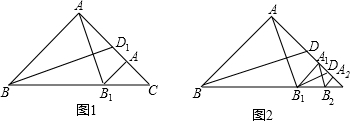
如图1,在Rt△ABC中,∠ABC=90°,∠B=30°,AD为BC边上的中线,E为AD上一动点,设DE=nEA,连接CE并延长交AB于点F,过点F作FG∥AC交AD(或延长线)于点G.
(1)当n=1时,则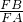 =______,
=______,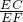 =______.
=______.
(2)如图2,当n= 时,求证:FG2=
时,求证:FG2= FE•FC;
FE•FC;
(3)如图3,当n=______时,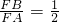 .
.
解:(1)当n=1时,E为AD的中点,
过点D作DH∥CF交AB于点H,
则BH=HF=FA,CF=2DH=2×2EF=4EF,
∴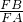 =2,
=2,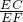 =3.
=3.
(2)过点D作DH∥CF交AB于点H,
设AF=x,则BH=HF=nx.
∵∠B=30°,
∴AC= AB=
AB= (2n+1)x,
(2n+1)x,
过点C作CM⊥AB于点M,
∵∠ACM=∠B=30°,
∴MC=ACcos∠ACM=ACcos30°= (2n+1)x•
(2n+1)x• =
= x,AM=
x,AM= AC=
AC= ×
× (2n+1)x=
(2n+1)x=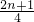 x,
x,
∴MF=AF-AM=x-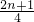 x=
x=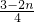 x,
x,
∴FC2=MF2+MC2=(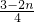 x)2+(
x)2+( x)2=
x)2= x2,
x2,
∵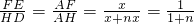 ,
,
∴FE= HD=
HD= FC,
FC,
∴FE•FC= FC2,
FC2, ,
,
∴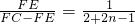 ,即
,即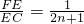 ,
,
∴当n= 时,FC2=
时,FC2= x2=x2,FE•FC=
x2=x2,FE•FC= FC2=
FC2= x2,
x2,
∴x2= FE•FC.
FE•FC.
∵FG∥AC,
∴ ,
,
∴FG=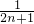 AC=
AC=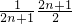 x=x,
x=x,
∴FC2=x2= FE•FC.
FE•FC.
(3)过点D作DH∥CF交AB于点H,
设BH=x,则HF=x,FA=4x,
∴ ,
,
∴n= .
.

分析:(1)首先过点D作DH∥CF交AB于点H,由n=1时,可得E为AD的中点,然后根据平行线分线段成比例定理,即可求得答案;
(2)首先过点D作DH∥CF交AB于点H,设AF=x,则BH=HF=nx.由∠B=30°,即可求得AC的值,然后过点C作CM⊥AB于点M,易求得MC与MF的值,由勾股定理即可求得FC2=MF2+MC2,然后由平行线分线段成比例定理,即可证得FG2= FE•FC;
FE•FC;
(3)过点D作DH∥CF交AB于点H,设BH=x,则HF=x,FA=4x,根据平行线分线段成比例定理,即可求得n的值.
点评:此题考查了平行线分线段成比例定理,三角函数的性质,勾股定理等知识.此题综合性较强,难度较大,解题的关键是注意方程思想与数形结合思想的应用.
过点D作DH∥CF交AB于点H,
则BH=HF=FA,CF=2DH=2×2EF=4EF,
∴
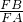 =2,
=2,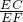 =3.
=3.(2)过点D作DH∥CF交AB于点H,
设AF=x,则BH=HF=nx.
∵∠B=30°,
∴AC=
 AB=
AB= (2n+1)x,
(2n+1)x,过点C作CM⊥AB于点M,
∵∠ACM=∠B=30°,
∴MC=ACcos∠ACM=ACcos30°=
 (2n+1)x•
(2n+1)x• =
= x,AM=
x,AM= AC=
AC= ×
× (2n+1)x=
(2n+1)x=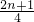 x,
x,∴MF=AF-AM=x-
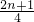 x=
x=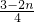 x,
x,∴FC2=MF2+MC2=(
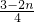 x)2+(
x)2+( x)2=
x)2= x2,
x2,∵
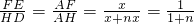 ,
,∴FE=
 HD=
HD= FC,
FC,∴FE•FC=
 FC2,
FC2, ,
,∴
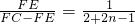 ,即
,即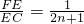 ,
,∴当n=
 时,FC2=
时,FC2= x2=x2,FE•FC=
x2=x2,FE•FC= FC2=
FC2= x2,
x2,∴x2=
 FE•FC.
FE•FC.∵FG∥AC,
∴
 ,
,∴FG=
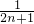 AC=
AC=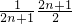 x=x,
x=x,∴FC2=x2=
 FE•FC.
FE•FC.(3)过点D作DH∥CF交AB于点H,
设BH=x,则HF=x,FA=4x,
∴
 ,
,∴n=
 .
.
分析:(1)首先过点D作DH∥CF交AB于点H,由n=1时,可得E为AD的中点,然后根据平行线分线段成比例定理,即可求得答案;
(2)首先过点D作DH∥CF交AB于点H,设AF=x,则BH=HF=nx.由∠B=30°,即可求得AC的值,然后过点C作CM⊥AB于点M,易求得MC与MF的值,由勾股定理即可求得FC2=MF2+MC2,然后由平行线分线段成比例定理,即可证得FG2=
 FE•FC;
FE•FC;(3)过点D作DH∥CF交AB于点H,设BH=x,则HF=x,FA=4x,根据平行线分线段成比例定理,即可求得n的值.
点评:此题考查了平行线分线段成比例定理,三角函数的性质,勾股定理等知识.此题综合性较强,难度较大,解题的关键是注意方程思想与数形结合思想的应用.

练习册系列答案
 名师指导期末冲刺卷系列答案
名师指导期末冲刺卷系列答案
相关题目