题目内容
如图,在四边形ABCD中,AD∥BC,点O在AD上,BO、CO分别平分∠ABC、∠DCB,若∠A+∠D=208°,求∠OBC+∠OCB的度数。请你将解答过程补充完整。
76°
解析试题分析:根据平行线的性质可得∠A+∠ABC=180°,∠D+∠DCB=180°,再根据角平分线的性质可得∠ABC=2∠OBC,∠DCB=2∠OCB,根据四边形的内角和定理可得∠A+∠D+2(∠OBC+∠OCB)=360°,然后结合∠A+∠D=208°即可求得结果.
解:∵AD∥BC
∴∠A+∠ABC=180°,∠D+∠DCB=180°
∵BO、CO分别平分∠ABC、∠DCB
∴∠ABC=2∠OBC,∠DCB=2∠OCB
∴∠A+∠D+2(∠OBC+∠OCB)=360°
∵∠A+∠D=208°
∴∠OBC+∠OCB=76°.
考点:平行线的性质,角平分线的性质
点评:平行线的判定和性质是初中数学的重点,贯穿于整个初中数学的学习,是中考中比较常见的知识点,一般难度不大,需熟练掌握.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
如图,在△ABC中,DE∥BC,若AD:AB=1:3,则△ADE与△ABC的面积之比是
| A.1:3 | B.1:4 | C.1:9 | D.1:16 |


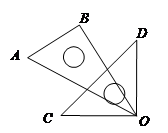

 ∠2,∠1+∠2=162°,求∠3与∠4的度数.
∠2,∠1+∠2=162°,求∠3与∠4的度数.
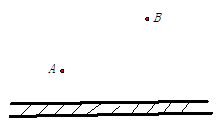

 、
、 被
被 、
、 所截,且
所截,且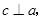

 ,求∠3的大小.
,求∠3的大小.