ĢāÄæÄŚČŻ
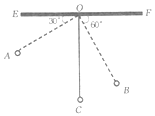
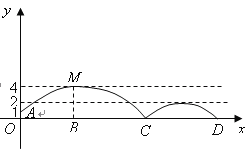
”¾ĢāÄæ”抔ĮĮŌŚŃ§Ļ°ÖŠÓöµ½ÕāŃłŅ»øöĪŹĢā£ŗ
ČēĶ¼£¬µć![]() ŹĒ»”
ŹĒ»”![]() ÉĻŅ»¶Æµć£¬Ļ߶Ī
ÉĻŅ»¶Æµć£¬Ļ߶Ī![]() µć
µć![]() ŹĒĻ߶Ī
ŹĒĻ߶Ī![]() µÄÖŠµć£¬¹żµć
µÄÖŠµć£¬¹żµć![]() ×÷
×÷![]() £¬½»
£¬½»![]() µÄŃÓ³¤ĻßÓŚµć
µÄŃÓ³¤ĻßÓŚµć![]() £®µ±
£®µ±![]() ĪŖµČŃüČż½ĒŠĪŹ±£¬ĒóĻ߶Ī
ĪŖµČŃüČż½ĒŠĪŹ±£¬ĒóĻ߶Ī![]() µÄ³¤¶Č£®
µÄ³¤¶Č£®

Š”ĮĮ·ÖĪö·¢ĻÖ£¬“ĖĪŹĢāŗÜÄŃĶعż³£¹ęµÄĶĘĄķ¼ĘĖć³¹µ×½ā¾ö£¬ÓŚŹĒ³¢ŹŌ½įŗĻѧĻ°ŗÆŹżµÄ¾ŃéŃŠ¾æ“ĖĪŹĢā£¬Ēė½«ĻĀĆęµÄĢ½¾æ¹ż³Ģ²¹³äĶźÕū£ŗ
![]() øł¾Żµć
øł¾Żµć![]() ŌŚ»”
ŌŚ»”![]() ÉĻµÄ²»Ķ¬Ī»ÖĆ£¬»³öĻąÓ¦µÄĶ¼ŠĪ£¬²āĮæĻ߶Ī
ÉĻµÄ²»Ķ¬Ī»ÖĆ£¬»³öĻąÓ¦µÄĶ¼ŠĪ£¬²āĮæĻ߶Ī![]() µÄ³¤¶Č£¬µĆµ½ĻĀ±ķµÄ¼ø×é¶ŌÓ¦Öµ£®
µÄ³¤¶Č£¬µĆµ½ĻĀ±ķµÄ¼ø×é¶ŌÓ¦Öµ£®
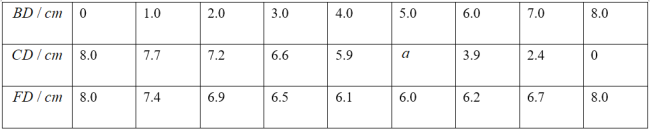
²Ł×÷ÖŠ·¢ĻÖ£ŗ
¢Ł"µ±µć![]() ĪŖ»”
ĪŖ»”![]() µÄÖŠµćŹ±£¬
µÄÖŠµćŹ±£¬ ![]() "£®ŌņÉĻÖŠ
"£®ŌņÉĻÖŠ![]() µÄÖµŹĒ
µÄÖµŹĒ
¢Ś"Ļ߶Ī![]() µÄ³¤¶ČĪŽŠč²āĮ漓æɵƵ½"£®Ēė¼ņŅŖĖµĆ÷ĄķÓÉ£»
µÄ³¤¶ČĪŽŠč²āĮ漓æɵƵ½"£®Ēė¼ņŅŖĖµĆ÷ĄķÓÉ£»
![]() ½«Ļ߶Ī
½«Ļ߶Ī![]() µÄ³¤¶Č×÷ĪŖ×Ō±äĮæ
µÄ³¤¶Č×÷ĪŖ×Ō±äĮæ![]() ŗĶ
ŗĶ![]() µÄ³¤¶Č¶¼ŹĒ
µÄ³¤¶Č¶¼ŹĒ![]() µÄŗÆŹż£¬·Ö±š¼ĒĪŖ
µÄŗÆŹż£¬·Ö±š¼ĒĪŖ![]() ŗĶ
ŗĶ![]() £¬²¢ŌŚĘ½ĆęÖ±½Ē×ų±źĻµ
£¬²¢ŌŚĘ½ĆęÖ±½Ē×ų±źĻµ![]() ÖŠ»³öĮĖŗÆŹż
ÖŠ»³öĮĖŗÆŹż![]() µÄĶ¼Ļó£¬ČēĶ¼ĖłŹ¾£®ĒėŌŚĶ¬Ņ»×ų±źĻµÖŠ»³öŗÆŹż
µÄĶ¼Ļó£¬ČēĶ¼ĖłŹ¾£®ĒėŌŚĶ¬Ņ»×ų±źĻµÖŠ»³öŗÆŹż![]() µÄĶ¼Ļó£»
µÄĶ¼Ļó£»
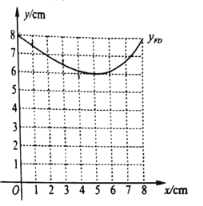
![]() ¼ĢŠųŌŚĶ¬Ņ»×ų±źĻµÖŠ»³öĖłŠčµÄŗÆŹżĶ¼Ļ󣬲¢½įŗĻĶ¼ĻóÖ±½ÓŠ“³ö£ŗµ±
¼ĢŠųŌŚĶ¬Ņ»×ų±źĻµÖŠ»³öĖłŠčµÄŗÆŹżĶ¼Ļ󣬲¢½įŗĻĶ¼ĻóÖ±½ÓŠ“³ö£ŗµ±![]() ĪŖµČŃüČż½ĒŠĪŹ±£¬Ļ߶Ī
ĪŖµČŃüČż½ĒŠĪŹ±£¬Ļ߶Ī![]() ³¤¶ČµÄ½üĖĘÖµ£®(½į¹ū±£ĮōŅ»Ī»Š”Źż)£®
³¤¶ČµÄ½üĖĘÖµ£®(½į¹ū±£ĮōŅ»Ī»Š”Źż)£®
”¾“š°ø”æ£Ø1£©¢Ł5.0£»¢Ś¼ū½āĪö£»£Ø2£©Ķ¼Ļó¼ū½āĪö£»£Ø3£©Ķ¼Ļó¼ū½āĪö£»3.5cm»ņ5.0cm»ņ6.3cm£»
”¾½āĪö”æ
£Ø1£©¢Łµć![]() ĪŖ»”
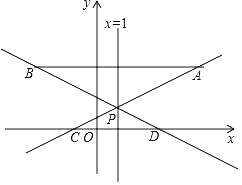
ĪŖ»”![]() µÄÖŠµćŹ±£¬”÷ABD”Õ”÷ACD£¬¼“æɵƵ½CD=BD£»¢ŚÓÉĢāŅāµĆ”÷ACF”Õ”÷ABD£¬¼“æɵƵ½CF=BD£»
µÄÖŠµćŹ±£¬”÷ABD”Õ”÷ACD£¬¼“æɵƵ½CD=BD£»¢ŚÓÉĢāŅāµĆ”÷ACF”Õ”÷ABD£¬¼“æɵƵ½CF=BD£»
£Ø2£©øł¾Ż±ķøńŹż¾ŻŌĖÓĆĆčµć·Ø¼“æÉ»³öŗÆŹżĶ¼Ļó£»
£Ø3£©»³ö![]() µÄĶ¼Ļ󣬵±
µÄĶ¼Ļ󣬵±![]() ĪŖµČŃüČż½ĒŠĪŹ±£¬·ÖĒéæöĢÖĀŪ£¬ČĪŅāĮ½±ß·Ö±šĻąµČŹ±£¬¼“ČĪŅāĮ½øöŗÆŹżĶ¼ĻóĻą½»Ź±µÄ½»µćŗį×ų±ź¼“ĪŖBDµÄ½üĖĘÖµ£®
ĪŖµČŃüČż½ĒŠĪŹ±£¬·ÖĒéæöĢÖĀŪ£¬ČĪŅāĮ½±ß·Ö±šĻąµČŹ±£¬¼“ČĪŅāĮ½øöŗÆŹżĶ¼ĻóĻą½»Ź±µÄ½»µćŗį×ų±ź¼“ĪŖBDµÄ½üĖĘÖµ£®
½ā£ŗ£Ø1£©¢Łµć![]() ĪŖ»”
ĪŖ»”![]() µÄÖŠµćŹ±£¬ÓÉŌ²µÄŠŌÖŹæÉµĆ£ŗ
µÄÖŠµćŹ±£¬ÓÉŌ²µÄŠŌÖŹæÉµĆ£ŗ
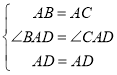 £¬
£¬
”ą”÷ABD”Õ”÷ACD£¬
”ąCD=BD=5.0£¬
”ą![]() £»
£»
¢Ś”ß![]() £¬
£¬
”ą![]() £¬
£¬
”ß £¬
£¬
”ą”÷ACF”Õ”÷ABD£¬
”ąCF=BD£¬
”ąĻ߶Ī![]() µÄ³¤¶ČĪŽŠč²āĮ漓æɵƵ½£»
µÄ³¤¶ČĪŽŠč²āĮ漓æɵƵ½£»
£Ø2£©ŗÆŹż![]() µÄĶ¼ĻóČēĶ¼ĖłŹ¾£ŗ
µÄĶ¼ĻóČēĶ¼ĖłŹ¾£ŗ
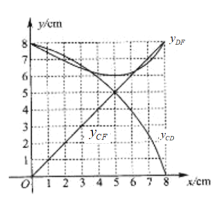
£Ø3£©ÓÉ£Ø1£©ÖŖ![]() £¬
£¬
»³ö![]() µÄĶ¼Ļó£¬ČēÉĻĶ¼ĖłŹ¾£¬µ±
µÄĶ¼Ļó£¬ČēÉĻĶ¼ĖłŹ¾£¬µ±![]() ĪŖµČŃüČż½ĒŠĪŹ±£¬
ĪŖµČŃüČż½ĒŠĪŹ±£¬
¢Ł![]() £¬BDĪŖ
£¬BDĪŖ![]() Óė
Óė![]() ŗÆŹżĶ¼ĻóµÄ½»µćŗį×ų±ź£¬¼“BD=5.0cm£»
ŗÆŹżĶ¼ĻóµÄ½»µćŗį×ų±ź£¬¼“BD=5.0cm£»
¢Ś![]() £¬BDĪŖ
£¬BDĪŖ![]() Óė
Óė![]() ŗÆŹżĶ¼ĻóµÄ½»µćŗį×ų±ź£¬¼“BD=6.3cm£»
ŗÆŹżĶ¼ĻóµÄ½»µćŗį×ų±ź£¬¼“BD=6.3cm£»
¢Ū![]() £¬BDĪŖ
£¬BDĪŖ![]() Óė
Óė![]() ŗÆŹżĶ¼ĻóµÄ½»µćŗį×ų±ź£¬¼“BD=3.5cm£»
ŗÆŹżĶ¼ĻóµÄ½»µćŗį×ų±ź£¬¼“BD=3.5cm£»
×ŪÉĻ£ŗµ±![]() ĪŖµČŃüČż½ĒŠĪŹ±£¬Ļ߶Ī
ĪŖµČŃüČż½ĒŠĪŹ±£¬Ļ߶Ī![]() ³¤¶ČµÄ½üĖĘÖµĪŖ3.5cm»ņ5.0cm»ņ6.3cm£®
³¤¶ČµÄ½üĖĘÖµĪŖ3.5cm»ņ5.0cm»ņ6.3cm£®

 ĆūŠ£æĪĢĆĻµĮŠ“š°ø
ĆūŠ£æĪĢĆĻµĮŠ“š°ø”¾ĢāÄæ”æĶعżæĪ±¾ÉĻ¶ŌŗÆŹżµÄѧĻ°£¬ĪŅĆĒ»żĄŪĮĖŅ»¶ØµÄ¾Ń飬ĻĀ±ķŹĒŅ»øöŗÆŹżµÄ×Ō±äĮæ![]() ÓėŗÆŹżÖµ
ÓėŗÆŹżÖµ![]() µÄ²æ·Ö¶ŌÓ¦Öµ£¬ĒėÄć½č¼ųŅŌĶłŃ§Ļ°ŗÆŹżµÄ¾Ń飬Ģ½¾æĻĀĮŠĪŹĢā£ŗ
µÄ²æ·Ö¶ŌÓ¦Öµ£¬ĒėÄć½č¼ųŅŌĶłŃ§Ļ°ŗÆŹżµÄ¾Ń飬Ģ½¾æĻĀĮŠĪŹĢā£ŗ
| ” | 0 | 1 | 2 | 3 | 4 | 5 | ” |
| ” | 6 | 3 | 2 | 1.5 | 1.2 | 1 | ” |
£Ø1£©µ±![]() Ź±£¬
Ź±£¬![]() £»
£»
£Ø2£©øł¾Ż±ķÖŠŹżÖµĆčµć![]() £¬²¢»³öŗÆŹżĶ¼Ļó£»
£¬²¢»³öŗÆŹżĶ¼Ļó£»
£Ø3£©¹Ū²ģ»³öµÄĶ¼Ļ󣬊“³öÕāøöŗÆŹżµÄŅ»ĢõŠŌÖŹ£ŗ £®