题目内容
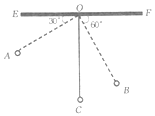
【题目】如图，物理教师为同学们演示单摆运动，单摆左右摆动中，在
的位置时俯角
，在
的位置时俯角
，若
，点
比点
高7
．
求：（1）单摆的长度；
（2）从点摆动到点经过的路径长．（要求：本题中的计算结果均保留整数．参考值：
；
）
【答案】（1）单摆的长度约19
；（2）从点
摆动到点
经过的路径长约
．
【解析】
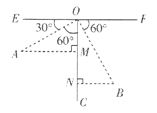
（1）如图（见解析），先根据角互余求出
，
，再分别解直角三角形的出OM、ON的长，然后根据
，利用线段的和差即可得；
（2）先求出
，再由题（1）的结论，利用弧长公式即可得．
（1）解：设单摆的长度为
如图，过作
于点
，过作
于点
在
中，
在
中，
由题知：
解得：
答：单摆的长度约19；
（2）由（1）知，，，
则从点到点经过的路径长为
答：从点摆动到点经过的路径长约．
华东师大版一课一练系列答案
【题目】某学校运动会的立定跳远和30秒跳绳两个单项比赛分成预赛和决赛两个阶段，下表为10名学生的预赛成绩，其中有三个数据模糊.
学生序号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
跳远（米） | 1.96 | 1.92 | 1.82 | 1.80 | 1.78 | 1.76 | 1.74 | 1.72 | 1.68 | 1.60 |
跳绳（次） | 63 |
| 75 | 60 | 63 | 72 | 70 |
|
| 65 |
在这10名学生中，进入立定跳远决赛的有8人，同时进入立定跳远决赛和30秒跳绳决赛的有6人，则（ ）
A.5号学生进入30秒跳绳决赛
B.2号学生进入30秒跳绳决赛
C.8号学生进入30秒跳绳决赛
D.9号学生进入30秒跳绳决赛
【题目】某垃圾处理厂，只能处理
、
两类垃圾，且每天只能处理其中的一类垃圾，已知该垃圾厂每月工作25天，每天处理垃圾种类的吨数及费用如下表：
|
| |
每天处理的吨数（单位：吨） | 22 | 30 |
每吨处理的费用（单位：元） | 150 | 100 |
设该垃圾厂每月处理类垃圾
天，这个厂每月处理垃圾的总吨数为
吨，每月处理垃圾所需的总费用为
元，据测算该厂每月最多处理垃圾590吨．
（1）求与的函数关系式；
（2）为何值时，最小，最小值是多少？
（3）一段时间后，由于改进了处理类垃圾的流程，使处理每吨类垃圾的费用减少了
元（
），类垃圾的处理费用没有改变，求该厂每月处理垃圾费用最少时，处理、两类垃圾的天数各是多少？