题目内容
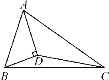
【题目】如图,⊙O的直径AB=2,C是弧AB的中点,AE,BE分别平分∠BAC和∠ABC,以E为圆心,AE为半径作扇形EAB,π取3,则阴影部分的面积为( )

A. ![]() ﹣4 B. 7
﹣4 B. 7![]() ﹣4 C. 6﹣
﹣4 C. 6﹣![]() D.
D. ![]()
【答案】A
【解析】
∵O的直径AB=2,
∴∠C=90°,
∵C是弧AB的中点,
∴![]() ,
,
∴AC=BC,
∴∠CAB=∠CBA=45°,
∵AE,BE分别平分∠BAC和∠ABC,
∴∠EAB=∠EBA=22.5°,
∴∠AEB=180°![]() (∠BAC+∠CBA)=135°,
(∠BAC+∠CBA)=135°,
连接EO,

∵∠EAB=∠EBA,
∴EA=EB,
∵OA=OB,
∴EO⊥AB,
∴EO为Rt△ABC内切圆半径,
∴S△ABC=![]() (AB+AC+BC)EO=
(AB+AC+BC)EO=![]() ACBC,
ACBC,
∴EO=![]() 1,
1,
∴AE2=AO2+EO2=12+(![]() 1)2=42
1)2=42![]() ,
,
∴扇形EAB的面积=![]() =
=![]() ,△ABE的面积=
,△ABE的面积=![]() ABEO=
ABEO=![]() 1,
1,
∴弓形AB的面积=扇形EAB的面积△ABE的面积=![]() ,
,
∴阴影部分的面积=![]() O的面积弓形AB的面积=
O的面积弓形AB的面积=![]() (
(![]() )=
)=![]() 4,
4,
故选:A.

练习册系列答案
相关题目