题目内容
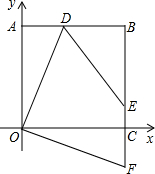 如图:正方形OABC中,B点的坐标为(2,2).D、E分别在边AB、BC上,F在BC的延长线上.且AD=CF,∠EDO=∠DOC.
如图:正方形OABC中,B点的坐标为(2,2).D、E分别在边AB、BC上,F在BC的延长线上.且AD=CF,∠EDO=∠DOC.
(1)猜想△OAD与△OCF能否通过旋转重合?请证明你的猜想.
(2)若D是AB的中点.求直线DE的解析线.
解:(1)△OAD与△OCF能通过旋转重合;
证明:在△OAD和△OCF中,
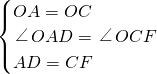 ,
,
∴△OAD≌△OCF,
∴OAD绕点O顺时针旋转90°与△OCF重合.
(2)∵D是AB的中点,
∴D(1,2),AD=CF=1,
设CE=x,则EF=EC+CF=x+1,BE=2-x,连接DF,
∵∠OFC=∠ODA=∠DOC=∠ODE,OD=OF,
∴∠ODF=∠OFD,
∴∠EDF=∠EFD,
∴DE=EF=x+1,
在Rt△BDE中,BD2+BE2=DE2,
∴1+(2-x)2=(x+1)2,
解得:x= ,
,
∴E(2, ),
),
设DE的解析式为:y=kx+b,
则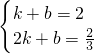 ,
,
解得: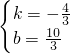 ,
,
∴直线DE的解析式为:y=- x+
x+ .
.
分析:(1)利用SAS可判定△OAD≌△OCF,继而结合图形可判断出答案.
(2)先求出点D坐标,设CE=x,则EF=EC+CF=EC+AD=x+1,BE=2-x,进而根据角的关系可确定DE的长度,在Rt△BDE中,利用勾股定理可解出x的值,继而得出点E的坐标,也可得出DE的解析式.
点评:此题考查了正方形的性质、待定系数法求函数解析式、勾股定理及旋转的性质,综合性较强,难度较大,解答本题的关键是熟练各基础知识点的应用,一步步解答.
证明:在△OAD和△OCF中,
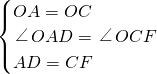 ,
,∴△OAD≌△OCF,
∴OAD绕点O顺时针旋转90°与△OCF重合.
(2)∵D是AB的中点,
∴D(1,2),AD=CF=1,
设CE=x,则EF=EC+CF=x+1,BE=2-x,连接DF,
∵∠OFC=∠ODA=∠DOC=∠ODE,OD=OF,
∴∠ODF=∠OFD,
∴∠EDF=∠EFD,
∴DE=EF=x+1,
在Rt△BDE中,BD2+BE2=DE2,
∴1+(2-x)2=(x+1)2,
解得:x=
 ,
,∴E(2,
 ),
),设DE的解析式为:y=kx+b,
则
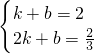 ,
,解得:
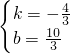 ,
,∴直线DE的解析式为:y=-
 x+
x+ .
.分析:(1)利用SAS可判定△OAD≌△OCF,继而结合图形可判断出答案.
(2)先求出点D坐标,设CE=x,则EF=EC+CF=EC+AD=x+1,BE=2-x,进而根据角的关系可确定DE的长度,在Rt△BDE中,利用勾股定理可解出x的值,继而得出点E的坐标,也可得出DE的解析式.
点评:此题考查了正方形的性质、待定系数法求函数解析式、勾股定理及旋转的性质,综合性较强,难度较大,解答本题的关键是熟练各基础知识点的应用,一步步解答.

练习册系列答案
 孟建平名校考卷系列答案
孟建平名校考卷系列答案
相关题目
 的垂线,垂足分别为E、F,并设矩形OEPF和正方形OABC不重合部分的面积为S.(提示:考虑点P在点B的左侧或右侧两种情况)
的垂线,垂足分别为E、F,并设矩形OEPF和正方形OABC不重合部分的面积为S.(提示:考虑点P在点B的左侧或右侧两种情况) 如图,正方形OABC、ADEF的顶点A,D,C在坐标轴上,点F在AB上,点B、E在函数
如图,正方形OABC、ADEF的顶点A,D,C在坐标轴上,点F在AB上,点B、E在函数 如图,正方形OABC和正方形ADEF的顶点A,D,C在坐标轴上,点F在AB上,点B,E在函数y=
如图,正方形OABC和正方形ADEF的顶点A,D,C在坐标轴上,点F在AB上,点B,E在函数y= 如图,正方形OABC与正方形ODEF是位似图形,O为位似中心,相似比为
如图,正方形OABC与正方形ODEF是位似图形,O为位似中心,相似比为 象上,点P(m,n)是函数
象上,点P(m,n)是函数