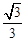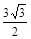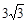题目内容
如图,A、B是⊙O的直径,C、D、E都是圆上的点,则∠1+∠2=___________
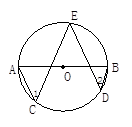
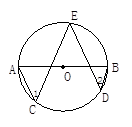
90°.
试题分析:首先连接OE,由在同圆或等圆中,同弧或等弧所对的圆周角等于这条弧所对的圆心角的一半,即可得∠1=
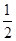 ∠AOE,∠2=
∠AOE,∠2=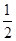 ∠BOE,即可得∠1+∠2=
∠BOE,即可得∠1+∠2=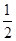 (∠AOE+∠BOE),则可求得∠1+∠2的度数.
(∠AOE+∠BOE),则可求得∠1+∠2的度数.试题解析:连接OE,
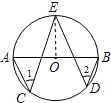
∵∠1=
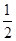 ∠AOE,∠2=
∠AOE,∠2=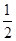 ∠BOE,
∠BOE,∴∠1+∠2=
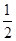 ∠AOE+
∠AOE+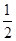 ∠BOE=
∠BOE=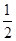 (∠AOE+∠BOE)=
(∠AOE+∠BOE)=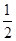 ×180°=90°.
×180°=90°.考点: 圆周角定理.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目


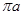 B.
B. 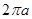 C.
C. 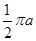 D.
D. 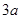
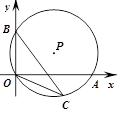
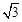 ,0)和点B(0,2), C是优弧
,0)和点B(0,2), C是优弧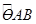 上的任意一点(不与点O,B重合),则tan∠BCO的值为( )
上的任意一点(不与点O,B重合),则tan∠BCO的值为( )