题目内容
某小区有一块直角三角形的绿地,量得两直角边AC=3米,BC=4米,考虑到这块绿地周围还有不少空余部分,于是打算将这块绿地扩充成等腰三角形,且扩充部分是以BC边为一直角边的直角三角形,求扩充后得到的等腰三角形绿地的周长(写出所有可能的情形).


(每种情况2分);
如图;
(1)当AB=BD=5米时;
由于BC⊥AD,则AC=CD=3米;
此时等腰三角形绿地的周长=5+5+3+3=16米;
(2)当AB=AD=5米时;
Rt△BCD中,CD=AD-AC=2米,BC=4米;
由勾股定理,得BD=
=2
米;
此时等腰三角形绿地的周长=5+5+2
=(10+2
)米;
(
不化简不扣分)
(3)当AD=BD时,设AD=BD=x米;
Rt△BCD中,BD=x米,CD=(x-3)米;
由勾股定理,得BD2=BC2+CD2,即(x-3)2+42=x2,解得x=
米;
此时等腰三角形绿地的周长=
×2+5=
米.
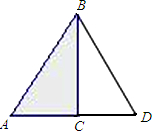
如图;
(1)当AB=BD=5米时;
由于BC⊥AD,则AC=CD=3米;
此时等腰三角形绿地的周长=5+5+3+3=16米;
(2)当AB=AD=5米时;
Rt△BCD中,CD=AD-AC=2米,BC=4米;
由勾股定理,得BD=
| BC2+CD2 |
| 5 |
此时等腰三角形绿地的周长=5+5+2
| 5 |
| 5 |
(
| 20 |
(3)当AD=BD时,设AD=BD=x米;
Rt△BCD中,BD=x米,CD=(x-3)米;
由勾股定理,得BD2=BC2+CD2,即(x-3)2+42=x2,解得x=
| 25 |
| 6 |
此时等腰三角形绿地的周长=
| 25 |
| 6 |
| 40 |
| 3 |


练习册系列答案
相关题目