题目内容
下列条件中,不能判断四边形ABCD是平行四边形的是( )
分析:根据平行四边形的判定:①两组对边分别平行的四边形是平行四边形;②两组对边分别相等的四边形是平行四边形;③一组对边平行且相等的四边形是平行四边形,对每个选项进行筛选可得答案.
解答: 解:A、AB∥CD,AB=CD,可以根据:一组对边平行且相等的四边形是平行四边形,判定四边形ABCD是平行四边形,故此选项不符合题意.
解:A、AB∥CD,AB=CD,可以根据:一组对边平行且相等的四边形是平行四边形,判定四边形ABCD是平行四边形,故此选项不符合题意.
B、AB=BC,AD=CD,不能判定四边形ABCD是平行四边形,故此选项符合题意;
C、∠A+∠B=180°,∠A=∠C则∠B+∠C=180°,∴AB∥CD,AD∥BC,可以判定四边形ABCD是平行四边形,故此选项不符合题意;
D、∠A=∠B=∠C=∠D,可判定四边形ABCD是矩形,故此选项不符合题意;
故选:B.
 解:A、AB∥CD,AB=CD,可以根据:一组对边平行且相等的四边形是平行四边形,判定四边形ABCD是平行四边形,故此选项不符合题意.
解:A、AB∥CD,AB=CD,可以根据:一组对边平行且相等的四边形是平行四边形,判定四边形ABCD是平行四边形,故此选项不符合题意.B、AB=BC,AD=CD,不能判定四边形ABCD是平行四边形,故此选项符合题意;
C、∠A+∠B=180°,∠A=∠C则∠B+∠C=180°,∴AB∥CD,AD∥BC,可以判定四边形ABCD是平行四边形,故此选项不符合题意;
D、∠A=∠B=∠C=∠D,可判定四边形ABCD是矩形,故此选项不符合题意;
故选:B.
点评:本题主要考查平行四边形的判定,关键是熟练掌握平行四边形的判定定理:
(1)两组对边分别平行的四边形是平行四边形;
(2)两组对边分别相等的四边形是平行四边形;
(3)一组对边平行且相等的四边形是平行四边形;
(4)两组对角分别相等的四边形是平行四边形;
(5)对角线互相平分的四边形是平行四边形.
(1)两组对边分别平行的四边形是平行四边形;
(2)两组对边分别相等的四边形是平行四边形;
(3)一组对边平行且相等的四边形是平行四边形;
(4)两组对角分别相等的四边形是平行四边形;
(5)对角线互相平分的四边形是平行四边形.

练习册系列答案
 一本好题口算题卡系列答案
一本好题口算题卡系列答案
相关题目
下列条件中,不能判断△ABC与△A′B′C′相似的是( )
| A、∠A=45°,∠C=26°,∠A′=45°,∠B′=109° | ||||||
B、AB=1,AC=
| ||||||
C、AB=1.5,AC=
| ||||||
D、AB=2,BC=1,∠C=90°,A′B′=
|
 4、如图所示,在下列条件中,不能判断△ABD≌△BAC的条件是( )
4、如图所示,在下列条件中,不能判断△ABD≌△BAC的条件是( )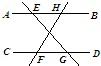 10、如图,下列条件中,不能判断直线AB∥CD的是( )
10、如图,下列条件中,不能判断直线AB∥CD的是( ) 如图,下列条件中,不能判断直线l1∥l2的是( )
如图,下列条件中,不能判断直线l1∥l2的是( )