题目内容
下列条件中,不能判断△ABC与△A′B′C′相似的是( )
| A、∠A=45°,∠C=26°,∠A′=45°,∠B′=109° | ||||||
B、AB=1,AC=
| ||||||
C、AB=1.5,AC=
| ||||||
D、AB=2,BC=1,∠C=90°,A′B′=
|
分析:考查相似三角形的判定问题,只要对应角相等,即形状相同,大小是没有限制的.
解答:解:A中对应角相等,所以可判断其相似,A正确;
B中三边对应成比例,即三角形的形状相同,所以相似,大小没有限制,比例常数是没有限制的,所以B对;
C中∠A相等,边长比确定,即形状确定,所以C也相似,正确;
D中对应角不相等,当A′C′=
时,才会相似,所以D错误.
故选D.
B中三边对应成比例,即三角形的形状相同,所以相似,大小没有限制,比例常数是没有限制的,所以B对;
C中∠A相等,边长比确定,即形状确定,所以C也相似,正确;
D中对应角不相等,当A′C′=
| 2 |
故选D.
点评:题中综合了多种情况的三角形相似,可以是对应角相等,也可以是一个角相等,但角的两边对应成比例,题中条件应认真分析,综合考虑.

练习册系列答案
相关题目
 4、如图所示,在下列条件中,不能判断△ABD≌△BAC的条件是( )
4、如图所示,在下列条件中,不能判断△ABD≌△BAC的条件是( )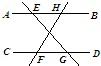 10、如图,下列条件中,不能判断直线AB∥CD的是( )
10、如图,下列条件中,不能判断直线AB∥CD的是( ) 如图,下列条件中,不能判断直线l1∥l2的是( )
如图,下列条件中,不能判断直线l1∥l2的是( )