题目内容
【题目】如图,将△ABC绕点B顺时针旋转60°得△DBE,点C的对应点E恰好落在AB延长线上,连接AD.下列结论一定正确的是()
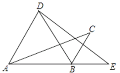
A. AD∥BC B. ∠CBE=∠C C. ∠ABD=∠E D. AD=BC
【答案】A
【解析】由题意易得∠ABD=∠CBE=60°,AB=BE,由此可得△ABD是等边三角形,从而可得∠ADB=60°,结合点E在AB的延长线上可得∠DBC=180°-60°-60°=60°即可得到∠ADB=∠DBC,由此可得AD∥BC,从而说明选项A正确;而由∠CBE是△ABC的外角,∠ABD是△BDE的外角可得∠CBE>∠C,∠ABD>∠E ,从而说明选项B、C不成立;由AD=AB,而AB![]() BC说明选项D不成立.
BC说明选项D不成立.
(1)∵△DBE是由△ABC绕点B旋转60°得到的,
∴∠ABD=∠CBE=60°,AB=DB,∠C=∠E,
∴△ABD是等边三角形,
∴∠ADB=60°,
∵点E在AB的延长线上,
∴∠DBC=180°-60°-60°=60°,
∴∠ADB=∠DBC,
∴AD∥BC,故选项A中结论成立;
(2)∵∠CBE是△ABC的外角,∠ABD是△BDE的外角,
∴∠CBE>∠C,∠ABD>∠E,故选项B和选项C中结论不成立;
(3)∵△ABD是等边三角形,
∴AD=AB,
∵在△ABD中,AB![]() BC,
BC,
∴AD![]() BC,故选项D中结论不成立.
BC,故选项D中结论不成立.
综上所述,只有A中结论成立,B、C、D中结论都不成立.
故选A.

练习册系列答案
相关题目