Question

【题目】已知，抛物线 y＝x2+bx+c 与 y 轴交于点 C，与 x 轴交于点 A 和点B（其中点 A 在 y 轴左侧，点 B 在 y 轴右侧），对称轴直线 x＝交 x 轴于点 H．

(1)若抛物线y＝x2+bx+c经过点（﹣4，6），求抛物线的解析式；

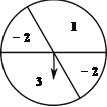
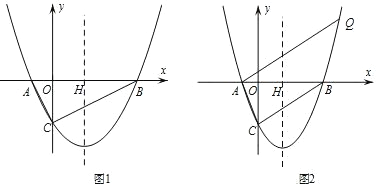
(2)如图1，∠ACB＝90°，点P是抛物线y＝x2+bx+c上位于y轴右侧的动点，且 S△ABP＝S△ABC，求点 P 的坐标；

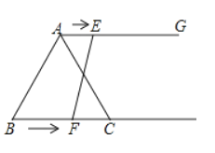
(3)如图 2，过点A作AQ∥BC交抛物线于点Q，若点Q的纵坐标为﹣c， 求点Q的坐标．

Answer 1

【答案】(1)y＝x2-x-8；(2)点 P 的坐标为（3，﹣2），（，2）；(3)点 Q 的坐标是（7，9）．

【解析】

(1)根据对称轴和点的坐标即可求出函数的解析式；

（2）连接 CH，利用交点式和韦达定理求出CH2及AB2

, 在 Rt△OHC 中，由勾股定理求出c的值，再分情况讨论即可.

（3）分别利用直线 BC和直线AC联系二次函数解析式消去y得到两个含k，c的方程，即可解出k，c的值，得出Q点坐标.

(1)∵抛物线 y＝x2+bx+c 的对称轴是直线 x＝，

∴﹣＝﹣b＝，

∴b＝﹣．

又抛物线 y＝ x2+bx+c 经过点（﹣4，6），

∴6＝×（﹣4）2﹣ ×（﹣4）+c， 解得 c＝﹣8．

故该抛物线解析式是 y ＝x2﹣ x﹣8；

如图 1，连接 CH，

∵对称轴直线 x＝交 x 轴于点 H，

∴AH＝BH，OH＝ ． 又∵∠ACB＝90°，

∴CH＝ AB，

设 A，B 两点的坐标分别为（x1，0），（x2，0），

则 x1，x2 是方程x2﹣ x+c＝0 的两根，

∴x1+x2＝3，x1x2＝2c，

∴AB2＝（x2﹣x1）2＝（x1+x2）2﹣4x1x2＝9﹣8c，

∴CH2＝ AB2＝ ﹣2c．

在 Rt△OHC 中，由勾股定理得：CH2＝OH2+OC2，即：c2+2c＝0， 解得：c＝﹣2 或 c＝0（舍去）．

∵S△ABP＝S△ABC，

∴|yP|＝|yC|＝2．

①当 yP＝﹣2 时，点 P 与点 C 关于直线 x＝对称，

∴P（3，﹣2）．

②当 yP＝2 时，x2﹣ x﹣2＝2， 解得：x＝．

又∵点 P 在 y 轴的右侧，

∴x＝ ，

∴点 P 的坐标为（ ，2）．综上所述，符合条件的点 P 的坐标为（3，﹣2），（，2）．

如图 2，设直线 BC 的解析式为：y＝kx+c（k≠0），联立直线 BC 与抛物线的解析式，得 ，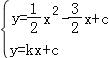

消去 y，得x2﹣ x+c＝kx+c， 解得：xC＝0，xB＝3+2k，

由(2)知 xA+xB＝3，

∴xA＝3﹣xB，

∴xA＝﹣2k．

把点 B 的坐标（3+2k，0）代入 y＝kx+c，得 c＝﹣k（3+2k）＝﹣3k﹣2k2．

∵AQ∥BC，

则设 AQ 的解析式为：y＝kx+m（k≠0）．联立直线 AQ 与抛物线的解析式，得

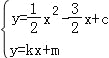
消去 y，得x2﹣ x+c＝kx+m，

设点 A、Q 的横坐标分别为 xA、xQ， 则 xA+xQ＝3+2k，

∵xA＝﹣2k，

∴xQ＝3+4k．

又∵yQ＝﹣ c，c＝﹣3k﹣2k2．

则有：﹣（﹣3k﹣2k2）＝（3+4k）2﹣（3+4k）+（﹣3k﹣2k2），解得：k1＝0（舍去），k2＝1，

∴c＝﹣3k﹣2k2＝﹣5，

∴点 Q 的坐标是（7，9）．