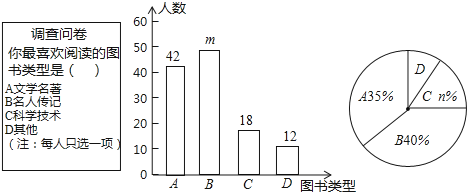
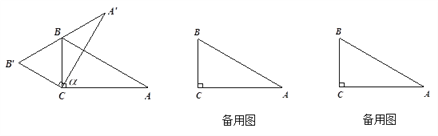
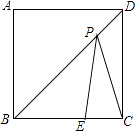
��Ŀ����
����Ŀ����������L��y=ax2+bx+c��a��b��c�dz�����abc��0����ֱ��l������y���ϵ�һ��P����������L�Ķ���Q��ֱ��l�ϣ���ƴ�ֱ��l���������L���С�һ��һ·����ϵ����ʱ��ֱ��l����������L�ġ����ߡ���������L����ֱ��l�ġ�·�ߡ���
��1����ֱ��y=mx+1��������y=x2��2x+n���С�һ��һ·����ϵ����m��n��ֵ��
��2����ij��·�ߡ�L�Ķ����ڷ���������y=![]() ��ͼ���ϣ����ġ����ߡ�l�Ľ���ʽΪy=2x��4����ˡ�·�ߡ�L�Ľ���ʽ��
��ͼ���ϣ����ġ����ߡ�l�Ľ���ʽΪy=2x��4����ˡ�·�ߡ�L�Ľ���ʽ��
��3��������k����![]() ��k��2ʱ����������L��y=ax2+��3k2��2k+1��x+k�ġ����ߡ�l��x�ᣬy����Χ�ɵ������������ȡֵ��Χ��
��k��2ʱ����������L��y=ax2+��3k2��2k+1��x+k�ġ����ߡ�l��x�ᣬy����Χ�ɵ������������ȡֵ��Χ��
���𰸡���1��m��ֵΪ��1��n��ֵΪ1����2��y=2��x+1��2��6��y=��![]() ��x��3��2+2����3��
��x��3��2+2����3��![]() ��S��
��S��![]() ��
��
��������
�����������1��ȷ��ֱ��y=mx+1��y��Ľ������꣬������������߽���ʽ�м������n��ֵ���ٸ��������ߵĽ���ʽ�ҳ��������꣬�������ֱ�߽���ʽ�м��ɵó����ۣ���2��ȷ��ֱ���뷴��������ͼ��Ľ������꣬�ɴ���������ߵĽ���ʽ������ֱ�ߵĽ���ʽ�ҳ�ֱ����x��Ľ������꣬������������߽���ʽ�м��ɵó����ۣ���3���������߽���ʽ�ҳ���������y��Ľ������꣬�ٸ��������ߵĽ���ʽ�ҳ��䶥�����꣬�����������ϴ���ϵ�������ɵó���������߶�Ӧ�ġ����ߡ�l�Ľ���ʽ���ҳ���ֱ����x��y��Ľ������꣬��������ε�����ҳ����S����k�Ĺ�ϵ�ϣ��ɶ��κ��������ʼ��ɵó����ۣ�
�����������1����ֱ��y=mx+1��x=0����y=1��
��ֱ����y��Ľ���Ϊ��0��1����
����0��1������������y=x2��2x+n��
��n=1��
�������ߵĽ���ʽΪy=x2��2x+1=��x��1��2��
�������ߵĶ�������Ϊ��1��0����
������1��0�����뵽ֱ��y=mx+1�У�
�ã�0=m+1����ã�m=��1��
��m��ֵΪ��1��n��ֵΪ1��
��2����y=2x��4���뵽y=![]() ���У�
����
2x��4=![]() ����2x2��4x��6=0��
����2x2��4x��6=0��
��ã�x1=��1��x2=3��
��á�·�ߡ�L�Ķ�������Ϊ����1����6������3��2����
����ߡ�l��y=2x��4��x=0����y=��4��
�ࡰ·�ߡ�L��ͼ�������0����4����
��á�·�ߡ�L�Ľ���ʽΪy=m��x+1��2��6��y=n��x��3��2+2��
��������4=m��0+1��2��6��4=n��0��3��2+2��
��ã�m=2��n=��![]() ��
��
��ˡ�·�ߡ�L�Ľ���ʽΪy=2��x+1��2��6��y=��![]() ��x��3��2+2��
��x��3��2+2��
��3����������L��y=ax2+��3k2��2k+1��x+k��x=0����y=k��
������������y��Ľ���Ϊ��0��k����
������L��y=ax2+��3k2��2k+1��x+k�Ķ�������Ϊ����![]() ��
��![]() ����
����
�衰���ߡ�l�Ľ���ʽΪy=px+k��
�ߵ�����![]() ��
��![]() ����y=px+k�ϣ�
����y=px+k�ϣ�
��![]() =��p
=��p![]() +k��
+k��
��ã�p=![]() ��
��
�ࡰ���ߡ�l�Ľ���ʽΪy=![]() x+k��
x+k��
��ࡰ���ߡ�l��y=![]() x+k��y=0����0=
x+k��y=0����0=![]() x+k��
x+k��
��ã�x=��![]() ��
��
�������ߡ�l��x��Ľ���Ϊ����![]() ��0������y��Ľ���Ϊ��0��k����
��0������y��Ľ���Ϊ��0��k����
�ࡰ���ߡ�l��x�ᣬy����Χ�ɵ����������S=![]() |��
|��![]() |��|k|��
|��|k|��
��![]() ��k��2��
��k��2��
��![]() ��
��![]() ��2��
��2��
��S=![]() =
=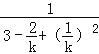 =
=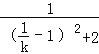 ��
��
��![]() =1ʱ��S�����ֵ�����ֵΪ
=1ʱ��S�����ֵ�����ֵΪ![]() ��
��
��![]() =2ʱ��S����Сֵ����СֵΪ
=2ʱ��S����Сֵ����СֵΪ![]() ��
��
��������L��y=ax2+��3k2��2k+1��x+k�ġ����ߡ�l��x�ᣬy����Χ�ɵ������������ȡֵ��ΧΪ![]() ��S��
��S��![]() ��
��

 ������ϰ�ο����뵥Ԫ���ϵ�д�
������ϰ�ο����뵥Ԫ���ϵ�д� �����Ծ���ĩ���100��ϵ�д�
�����Ծ���ĩ���100��ϵ�д�