题目内容
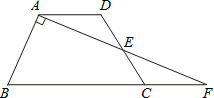
已知,如图,在□ABCD中,E、F分别为边AB、CD的中点,BD是对角线,AG∥DB交CB的延长线于G.
(1)求证:△ADE≌△CBF;
(2)若四边形BEDF是菱形,则四边形AGBD是什么特殊四边形?并证明你的结论.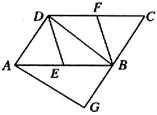
(1)求证:△ADE≌△CBF;
(2)若四边形BEDF是菱形,则四边形AGBD是什么特殊四边形?并证明你的结论.

证明:(1)因为ABCD是平行四边形
所以AD=BC,∠A=∠C,AB=CD
又因为E、F分别为边AB、CD的中点,
所以AE=CF
所以△ADE≌△CBF (SAS)
(2)因为ABCD是平行四边形
AD∥BG,又知AG∥DB
所以四边形AGBD是平行四边形,
四边形BEDF是菱形,
所以DE=BE=AE,
所以∠DAE=∠ADE,∠EDB=∠DBE
2∠ADE+2∠EDB=180°
所以∠ADE+∠EDB=90°
四边形AGBD是矩形(有一个角是直角的平行四边形是矩形)
所以AD=BC,∠A=∠C,AB=CD
又因为E、F分别为边AB、CD的中点,
所以AE=CF
所以△ADE≌△CBF (SAS)
(2)因为ABCD是平行四边形
AD∥BG,又知AG∥DB
所以四边形AGBD是平行四边形,
四边形BEDF是菱形,
所以DE=BE=AE,
所以∠DAE=∠ADE,∠EDB=∠DBE
2∠ADE+2∠EDB=180°
所以∠ADE+∠EDB=90°
四边形AGBD是矩形(有一个角是直角的平行四边形是矩形)
(1)在证明全等时常根据已知条件,分析还缺什么条件,然后用(SAS,ASA,SSS)来证明全等;(2)先由菱形的性质得出AE=BE=DE,再通过角之间的关系求出∠ADE+∠EDB=90°即∠ADB=90°,所以判定四边形AGBD是矩形.

练习册系列答案
相关题目
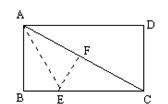
 ABCD中 ,E是BC的中点,且∠AEC=∠DCE,下列结论中正确的有
ABCD中 ,E是BC的中点,且∠AEC=∠DCE,下列结论中正确的有 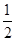 DF 2.S△AFD=2S△EFB
DF 2.S△AFD=2S△EFB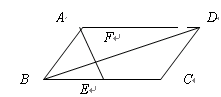

 ABCD 中, AB
ABCD 中, AB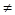 AD ,对角线 AC 与 BD 相交于点 O , OE⊥BD交 AD 于 E ,若△ABE 的周长为 12cm ,则
AD ,对角线 AC 与 BD 相交于点 O , OE⊥BD交 AD 于 E ,若△ABE 的周长为 12cm ,则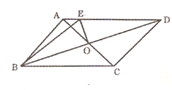
 的正方形覆盖
的正方形覆盖 的正方形网格,最多覆盖边长为
的正方形网格,最多覆盖边长为



