题目内容
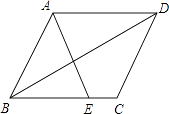
【题目】如图，四边形ABCD是平行四边形，DE平分∠ADC交AB于点E，BF平分∠ABC，交CD于点F． 
（1）求证：DE=BF；
（2）连接EF，写出图中所有的全等三角形．（不要求证明）
【答案】
（1）证明：∵四边形ABCD是平行四边形，
∴DC∥AB，
∴∠CDE=∠AED，
∵DE平分∠ADC，
∴∠ADE=∠CDE，
∴∠ADE=∠AED，
∴AE=AD，
同理可得CF=CB，
又∵AD=CB，
∴AE=CF，
∵AB=CD，
∴DF=BE，
∴四边形DEBF是平行四边形，
∴DE=BF
（2）证明：△ADE≌△CBF，△DFE≌△BEF．
【解析】（1）由平行四边形的性质和已知条件证明四边形DEBF是平行四边形，根据平行四边形的性质可得到DE=BF；（2）连接EF，则图中所有的全等三角形有：△ADE≌△CBF，△DFE≌△BEF．
练习册系列答案
名校课堂系列答案
相关题目
【题目】已知甲、乙两种原料中均含有A元素，其含量及每吨原料的购买单价如下表所示：
A元素含量 | 单价（万元/吨） | |
甲原料 | 5% | 2.5 |
乙原料 | 8% | 6 |
已知用甲原料提取每千克A元素要排放废气1吨，用乙原料提取每千克A元素要排放废气0.5吨，若某厂要提取A元素20千克，并要求废气排放不超过16吨，问：该厂购买这两种原料的费用最少是多少万元？
