题目内容
【题目】如图所示,在 
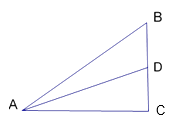
（1）比较∠BAD和∠DAC的大小。
（2）求sin∠BAD
【答案】
（1）
解：过点D做AB的垂线，垂足记为E，
∴sin∠BAD=
;sin∠DAC=
;
∵ED＜BD=DC;
∴sin∠BAD＜sin∠DAC;
∴∠BAD＜∠DAC＜90°;
（2）
解：由勾股定理求出AB=
，AD=
;
又∵
=
BD.AC=AB.DE,
∴×1×3=××DE,
∴DE=
∴sin∠BAD=
【解析】(1)过点D做AB的垂线，垂足记为E，再根据正弦的定义和大边对大角的关系得出答案。
(2)由勾股定理求出AB=
，AD=
，再根据三角形的面积公式求出DE，最后根据正弦的定义求出答案。
【考点精析】利用锐角三角函数的定义对题目进行判断即可得到答案，需要熟知锐角A的正弦、余弦、正切、余切都叫做∠A的锐角三角函数．
练习册系列答案
相关题目
