��Ŀ����
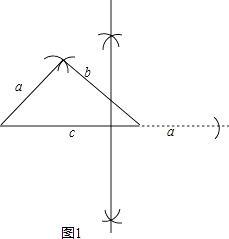
����Ŀ��������������ߵij�a��b��c���� ![]() =b����ô���ǾͰ������������ν������ȳ������Ρ����磺���߳��ֱ�Ϊ1��1��1��3��5��7�����������ζ��ǡ��ȳ������Ρ���
=b����ô���ǾͰ������������ν������ȳ������Ρ����磺���߳��ֱ�Ϊ1��1��1��3��5��7�����������ζ��ǡ��ȳ������Ρ��� 
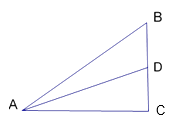
��1����ͼ1����֪�����߶εij��ֱ�Ϊa��c��a��c������ֱ�ߺ�Բ����һ����̱ߡ���ߵij��ֱ�Ϊa��c�ġ��ȳ������Ρ�����д������������ͼ�ۼ�����
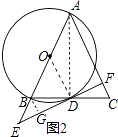
��2����ͼ2����ABC�У�AB=AC����ABΪֱ���ġ�O��BC�ڵ�D������D����O�����߽�AB�ӳ����ڵ�E����AC�ڵ�F���� ![]() ���жϡ�AEF�Ƿ�Ϊ���ȳ������Ρ�����˵�����ɣ�
���жϡ�AEF�Ƿ�Ϊ���ȳ������Ρ�����˵�����ɣ�
���𰸡�
��1���⣺����ͼ�Σ�����ͼ1��ʾ��
��2���⣺��AEF�ǡ��ȳ������Ρ���
���ɣ�����AD��OD������ͼ2��ʾ��
��AB�ǡ�O��ֱ����
��AD��BC��
��AB=AC��
���D��BC���е㣬
�ߵ�OΪAB���е㣬
��OD��AC��
��DF�С�O�ڵ�D��
��OD��DF��
��EF��AF��
����B��BG��EF�ڵ�G��
�ߡ�BGD=��CFD=90�㣬��BDG=��CDF��BD=CD��
���BGD�ա�CFD��ASA����
��BG=CF��
�� ![]() ��
��
�� ![]() ��
��
��BG��AF��
�� ![]() ��
��
��Rt��AEF�У���AE=5k��AF=3k���ɹ��ɶ����ã�EF=4k��
�� ![]() ��
��
���AEF�ǡ��ȳ������Ρ���
����������1������������Ի�����Ӧ��ͼ�Σ�������Խ������2�����ݡ��ȳ������Ρ��Ķ��壬����Ŀ����Ϣ�ģ��������ߵ����ʣ����������ε����ʣ������ε�ȫ���Լ����ɶ��������жϡ�AEF�Ƿ�Ϊ���ȳ������Ρ���