题目内容
一家图文广告公司制作的宣传画板颇受商家欢迎,这种画板的厚度忽略不计,形状均为正方形,边长在10~30dm之间.每张画板的成本价(单位:元)与它的面积(单位:dm2)成正比例,每张画板的出售价(单位:元)由基础价和浮动价两部分组成,其中基础价与画板的大小无关,是固定不变的.浮动价与画板的边长成正比例.在营销过程中得到了表格中的数据.
| 画板的边长(dm) | 10 | 20 |
| 出售价(元/张) | 160 | 220 |
(2)已知出售一张边长为30dm的画板,获得的利润为130元(利润=出售价-成本价),
①求一张画板的利润与边长之间满足的函数关系式;
②当边长为多少时,出售一张画板所获得的利润最大?最大利润是多少?
(1)y=6x+100;(2)W=-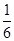 x2+6x+100,154.
x2+6x+100,154.
解析试题分析:(1)每张画板的成本价与它的面积成正比例,可设其解析式为y成本价=ax2,每张画板的出售价由基础价和浮动价两部分组成,其中基础价与画板的大小无关,是固定不变的.浮动价与画板的边长成正比例.可设y出售价=kx+b.把表中数据代入即可求出结论;
(2)由y利润=y出售价-y成本价,可得出二次函数,求出其最大值即可.
试题解析:(1)设正方形画板的边长为xdm,出售价为每张y元,且y=kx+b(k≠0) (1分)
由表格中的数据可得,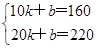 ,解得
,解得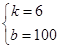
从而一张画板的出售价y与边长x之间满足函数关系式y=6x+100
(2)设每张画板的成本价为ax2,利润W=6x+100-ax2
当x=30时,W=130,180+100-900a=130,得a=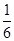
一张画板的利润W与边长x之间满足函数关系式W=-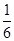 x2+6x+100
x2+6x+100
由W=-16(x-18)2+154,知当x=18时,W有最大值,W最大=154
因此当正方形画板的边长为18dm时,可获最大利润154元.
考点: 1.一次函数表达式;2.二次函数表达式;3.二次函数的最大值.

许多家庭以燃气作为烧水做饭的燃料,节约用气是我们日常生活中非常现实的问题.某款燃气灶旋转位置从0度到90度(如图),燃气关闭时,燃气灶旋转的位置为0度,旋转角度越大,燃气流量越大,燃气开到最大时,旋转角度为90度.为测试燃气灶旋转在不同位置上的燃气用量,在相同条件下,选择燃气灶旋钮的5个不同位置上分别烧开一壶水(当旋钮角度太小时,其火力不能够将水烧开,故选择旋钮角度x度的范围是18≤x≤90),记录相关数据得到下表:
| 旋钮角度(度) | 20 | 50 | 70 | 80 | 90 |
| 所用燃气量(升) | 73 | 67 | 83 | 97 | 115 |
(1)请你从所学习过的一次函数、反比例函数和二次函数中确定哪种函数能表示所用燃气量y升与旋钮角度x度的变化规律?说明确定是这种函数而不是其它函数的理由,并求出它的解析式;
(2)当旋钮角度为多少时,烧开一壶水所用燃气量最少?最少是多少?
(3)某家庭使用此款燃气灶,以前习惯把燃气开到最大,现采用最节省燃气的旋钮角度,每月平均能节约燃气10立方米,求该家庭以前每月的平均燃气量.

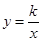 的图象交于A(-2,6)和点B(4,n)
的图象交于A(-2,6)和点B(4,n)

 与
与 是反比例函数
是反比例函数 图象上的两个点.
图象上的两个点.
 的取值范围.
的取值范围. 的图象的两个交点.
的图象的两个交点.
 轴的交点C的坐标及△AOB的面积;
轴的交点C的坐标及△AOB的面积;
 的图象与
的图象与 轴交点的纵坐标为-2,且与两坐标轴围成的直角三角形面积为1,试确定此一次函数的表达式.
轴交点的纵坐标为-2,且与两坐标轴围成的直角三角形面积为1,试确定此一次函数的表达式.