��Ŀ����
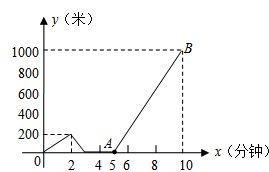
B��λ����Ȼ������������ɳȺ��,ʢ����������.A�ۡ�B����C��������ͬһ��ֱ����,һ�洬��A�۳�������B����C�ۺ���,����2Сʱʱ������Ⱥ,�����洬���ٻ�����B�۷���ǰ�д���.���洬����һСʱ��,һ�ҿ�ͧ��C�۳���,����B��ǰ��A����������.����ͧ����B��ʱ�洬ǡ�ô������,�洬����ԭ�پ���B������C��.������������B�۵ľ���y(����)���洬����ʱ��x(Сʱ)�ĺ���ͼ��,���ͼ��ش��������⣺
��1����ֱ��д��m,a��ֵ��
��2������߶�MN�Ľ���ʽ,��д���Ա�����ȡֵ��Χ.
��3�����洬������ڼ�Сʱ�������10����?
��1��m=20,a=11�� ��2��yMN=��20x+60 (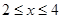 );(3)���洬�������
);(3)���洬�������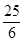 Сʱ�������10���
Сʱ�������10���
���������������1������������B�۵ľ���y��������洬����ʱ��x��Сʱ���ĺ���ͼ�����������m��a��ֵ���ɣ�
��2����yMN=kx+b����M��N����������k��b��ֵ������ȷ�����߶�MN�Ľ���ʽ����д���Ա�����ȡֵ��Χ���ɣ�
��3����yNG=px+q����N��Q����������p��q��ֵ����yEF=cx+d����E��F�������c��d��ֵ�������������10�����г�����x�ķ��̣�������̵Ľ⼴�ɵõ������
�����������1��m=20,a=11��
��2����yMN=kx+b���ɵ�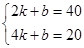 ����
����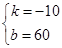
��ã�yMN=��20x+60 (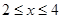 )
)
��ֱ��BC�Ľ���ʽΪyMN=��20x+60��
��3����yNG=kx+b���ɵ� ����
����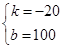
��ã�yNG=��20x+100
��yEF=kx+b���ɵ�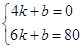 ����
����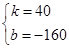
��ã�yEF=40x��160
��20x+100��(40x��160)=10
���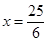
�𣺴��洬�������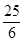 Сʱ�������10���
Сʱ�������10���
���㣺һ�κ�����Ӧ�ã�

һ��ͼ�Ĺ�湫˾�������������������̼һ�ӭ�����ֻ���ĺ�Ⱥ��Բ��ƣ���״��Ϊ�����Σ��߳���10��30dm֮�䣮ÿ�Ż���ijɱ��ۣ���λ��Ԫ���������������λ��dm2������������ÿ�Ż���ij��ۼۣ���λ��Ԫ���ɻ����ۺ�������������ɣ����л������뻭��Ĵ�С�أ��ǹ̶�����ģ��������뻭��ı߳�������������Ӫ�������еõ��˱����е����ݣ�
| ����ı߳���dm�� | 10 | 20 |
| ���ۼۣ�Ԫ/�ţ� | 160 | 220 |
��2����֪����һ�ű߳�Ϊ30dm�Ļ��壬��õ�����Ϊ130Ԫ�������ۼۣ��ɱ��ۣ���
����һ�Ż����������߳�֮������ĺ�����ϵʽ��
�ڵ��߳�Ϊ����ʱ������һ�Ż�������õ����������������Ƕ��٣�

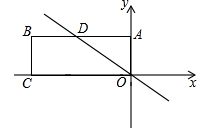
 ��4x+3��ͼ��x����A��B���㣨��A�ڵ�B����ࣩ�� ��y���ڵ�C.
��4x+3��ͼ��x����A��B���㣨��A�ڵ�B����ࣩ�� ��y���ڵ�C.
 ��ͼ���뷴��������
��ͼ���뷴�������� ��ͼ����A(1��4)��B(��2��m)���㣬
��ͼ����A(1��4)��B(��2��m)���㣬  �Ľ⼯��
�Ľ⼯�� Ԫ������������˾���������
Ԫ������������˾��������� Ԫ.���
Ԫ.���
 �֣�Ӧ��ˮ��
�֣�Ӧ��ˮ�� Ԫ��
Ԫ��