题目内容
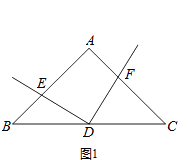
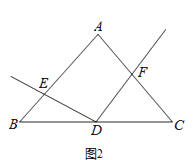
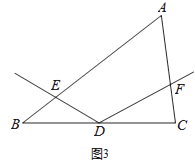
【题目】如图,某数学兴趣小组的同学利用标杆测量旗杆(AB)的高度:将一根5米高的标杆(EF)竖在某一位置,有一名同学站在一处与标杆、旗杆成一条直线,此时他看到标杆顶端与旗杆顶端重合,另外一名同学测得站立的同学离标杆3米,离旗杆30米.如果站立的同学的眼睛距地面(CD)1.6米,求旗杆的高度. 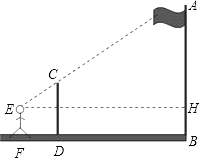
【答案】解:过点E作EH⊥AB于点H,交CD于点G. 由题意可得 四边形EFDG、GDHB都是矩形,AB∥CD∥EF.
∴△AECG∽△EAH.
∴ ![]() .
.
由题意可得
EG=FD=3,GH=BD=30,CG=CD﹣GD=CD﹣EF=5﹣1.6=3.4.
∴ ![]() .
.
∴AH=34米.
∴AH=AH+HB=34+1.6=35.6米.
答:旗杆高ED为35.6米.
【解析】过点E作CG⊥AH于点H,交CD于点G得出△EGC∽△EHA,进而求出AH的长,进而求出AB的长.
【考点精析】解答此题的关键在于理解相似三角形的应用的相关知识,掌握测高:测量不能到达顶部的物体的高度,通常用“在同一时刻物高与影长成比例”的原理解决;测距:测量不能到达两点间的举例,常构造相似三角形求解.

练习册系列答案
 新思维假期作业寒假吉林大学出版社系列答案
新思维假期作业寒假吉林大学出版社系列答案
相关题目
【题目】“2018年西安女子半程马拉松”的赛事有两项:A“女子半程马拉松”;B、“5公里女子健康跑”.小明对部分参赛选手作了如下调查:
调查总人数 | 50 | 100 | 200 | 300 | 400 | 500 |
参加“5公里女子健康跑”人数 | 18 | 45 | 79 | 120 | 160 | b |
参加“5公里女子健康跑”频率 | 0.360 | a | 0.395 | 0.400 | 0.400 | 0.400 |

(1)计算表中a,b的值;
(2)在图中,画出参赛选手参加“5公里女子健康跑“的频率的折线统计图;
(3)从参赛选手中任选一人,估计该参赛选手参加“5公里女子健康跑”的概率(精确到0.1).