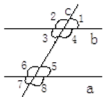��Ŀ����
����Ŀ������ѧ�Ķ���
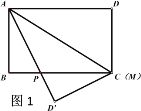
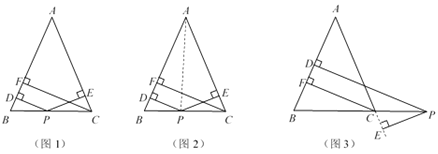
��ͼ1������ABC�У�AB��AC����PΪ��BC�ϵ�����һ�㣬����P��PD��AB��PE��AC������ֱ�ΪD��E������C��CF��AB������ΪF����֤��PD��PE��CF��
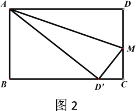
СҢ��֤��˼·������ͼ2������AP������ABP����ACP���֮�͵�����ABC���������֤����PD��PE��CF��
���ƹ�������
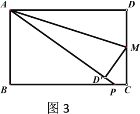
��ͼ3������P��BC�ӳ�����ʱ�������������䣬��������������������۵ľ���ͷ���������PD��PE��CF��������ϵ����֤����
�����������
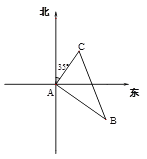
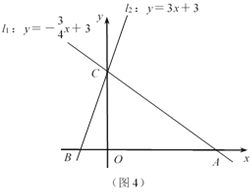
��ͼ4����ƽ��ֱ������ϵ��������ֱ��l1��y����![]() x��3��l2��y��3x��3��l1��l2��x��Ľ���ֱ�ΪA��B��
x��3��l2��y��3x��3��l1��l2��x��Ľ���ֱ�ΪA��B��
(1)����ֱ�ߵĽ���C������Ϊ ��
(2)˵����ABC�ǵ��������Σ�
(3)��l2�ϵ�һ��M��l1�ľ�����1����������Ľ��ۣ����M�����꣮
���𰸡����ƹ����������룺PD��PE��CF��֤���������������������(1)C(0��3)��(2)֤����������(3)M(��![]() ��2)��M(
��2)��M(![]() ��4)��
��4)��
��������
���ƹ��������������⣬���룺PD��PE��CF,��S��APB��S��ACP��S��ABC��������. �����������(1)����ֱ���ཻ֪�����������飬�õ�C������; (2)���ݷ����齫A,B���������AB�߶γ����ɹ��ɶ�����AC�߶γ�������֤����ABC�ǵ��������Σ���3�������������۵�ME�߶γ����ɴ˵õ�M�������.
�ƹ�����
���룺PD��PE��CF��
֤������ͼ������AP��
�� S��APB��S��ACP��S��ABC����
�� ![]() AB��PD��
AB��PD��![]() AC��PE��
AC��PE��![]() AB��CF��
AB��CF��
�� AB��AC��
�� PD��PE��CF��
�������
(1)C(0��3)��
(2)l1��y����![]() x��3����y��0����x��4����A(4��0)��
x��3����y��0����x��4����A(4��0)��
l2��y��3x��3����y��0����x����1����B(��1��0)��
�� AB��5��
��Rt��AOC�У���AOC��90�㣬
�� AC2��AO2��CO2 ����AC��5��
�� AB��AC��5���� ��ABC�ǵ�����������
(3)��M��ֱ���MD��AC��ME��AB������ֱ�ΪD��E��
������Ľ��۵ã�ME��MD��CO��ME��MD��CO��
�� ME��2��ME��4���� M(��![]() ��2)��M(
��2)��M(![]() ��4)��
��4)��

 ��ʦָ����ĩ��̾�ϵ�д�
��ʦָ����ĩ��̾�ϵ�д� �����ܿ����ϵ�д�
�����ܿ����ϵ�д�