题目内容
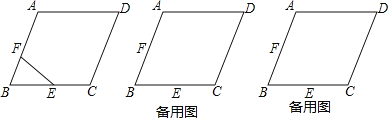
【题目】已知,如图,在边长为10的菱形ABCD中,cos∠B=![]() ,点E为BC边上的中点,点F为边AB边上一点,连接EF,过点B作EF的对称点B′,
,点E为BC边上的中点,点F为边AB边上一点,连接EF,过点B作EF的对称点B′,
(1)在图(1)中,用无刻度的直尺和圆规作出点B′(不写作法,保留痕迹);
(2)当△EFB′为等腰三角形时,求折痕EF的长度.
(3)当B′落在AD边的中垂线上时,求BF的长度.
【答案】(1)尺规作图见解析;(2)EF=5或![]() 或
或![]() ;(3)
;(3)![]() .
.
【解析】
试题(1)分别以F、E为圆心,FB、EB为半径画弧,两弧交于点B,B即为所求;
(2)分情况①当BE=EF时,②BE=BF时,③EF=BF时讨论即可;
(3)连接BB,FE,可知BB⊥FE,依据翻折及勾股定理即可解得.
试题解析:(1)尺规作图:
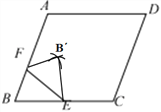
(2)由翻折知:△FBE≌△FBE,
∴BE=BE,BF=BF,
∵点E为BC边上的中点,
∴BE=BE=5,
① 当BE=EF时,EF=5,
②当BE=BF时,过点F作FG⊥BE于点G,
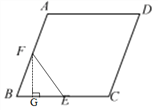
在Rt△FBG中,BE=BF=5,cos∠B=![]() ,
,
∴BG=![]() ,GE=BE-BG=
,GE=BE-BG=![]() ,
,
FG=![]() ,
,
在Rt△FEG中,FE=![]() ;
;
③当EF=BF时,
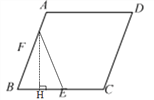
过点F作FH⊥BE于点H,BH=![]() BE=
BE=![]() ,
,
在Rt△FBH中, cos∠B=![]() ,
,
∴BF=BH×![]() =
=![]() ,
,
∴EF=![]() ,
,
综上:EF=5或![]() 或
或![]() .
.
(3)
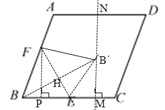
如图:连接BB,FE,交点 为H,
则BB⊥FE,
∵AN=DN=BE=CE=5,
∴EM=3,BE=BE=5,
∴BM=4,MN=![]() ,
,
BH=![]() ,
,
∴BF=BF=![]() .
.

 中考解读考点精练系列答案
中考解读考点精练系列答案【题目】如图,五边形![]() 内部有若干个点,用这些点以及五边形
内部有若干个点,用这些点以及五边形![]() 的顶点
的顶点![]() 的顶点把原五边形分割成一些三角形(互相不重叠):
的顶点把原五边形分割成一些三角形(互相不重叠):

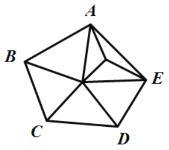
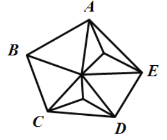
内部有1个点 内部有2个点 内部有3个点
(1)填写下表:
五边形 | 1 | 2 | 3 | 4 | … | n |
分割成的三角形的个数 | 5 | 7 | 9 | … |
(2)原五边形能否被分割成2019个三角形?若能,求此时五边形![]() 内部有多少个点?若不能,请说明理由.
内部有多少个点?若不能,请说明理由.