题目内容
【题目】如图,已知![]() 的半径为
的半径为![]() ,
,![]() 与
与![]() 外切于点
外切于点![]() ,经过点
,经过点![]() 的直线与
的直线与![]() 、
、![]() 分别交于点
分别交于点![]() 、
、![]() ,
,![]() .
.

(1)求![]() 的长;
的长;
(2)当![]() 时,求
时,求![]() 的半径.
的半径.
【答案】(1)![]() ;(2)
;(2)![]() 的半径为
的半径为![]() .
.
【解析】
(1)作OM⊥AB于M,如图,在Rt△OAM中根据正切定义得到tan∠OAM=![]() =
=![]() ,则设OM=
,则设OM=![]() x,AM=2x,由勾股定理得OA=5x,所以5x=5,解得x=1,于是得到AM=2,OM=
x,AM=2x,由勾股定理得OA=5x,所以5x=5,解得x=1,于是得到AM=2,OM=![]() ,然后根据垂径定理得到AB=2AM=4;
,然后根据垂径定理得到AB=2AM=4;
(2)作PN⊥AC于N,如图,则AN=CN,设⊙P的半径为r,先证明△PAN∽△OAM,利用相似比得到AN=![]() r,则AC=2AN=
r,则AC=2AN=![]() r,在Rt△OMC中,根据勾股定理得到OC2(
r,在Rt△OMC中,根据勾股定理得到OC2(![]() )2+(
)2+(![]() r+2)2,再证明△OAC∽△OCP,利用相似比得到OC2=OAOP=5(5+r),则(
r+2)2,再证明△OAC∽△OCP,利用相似比得到OC2=OAOP=5(5+r),则(![]() )2+(
)2+(![]() r+2)2=5(5+r),然后解r的方程即可.
r+2)2=5(5+r),然后解r的方程即可.
(1)作![]() 于
于![]() ,如图,
,如图,
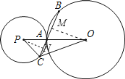
在![]() 中,
中,![]() ,
,
设![]() ,
,![]() ,
,
∴![]() ,
,
∴![]() ,解得
,解得![]() ,
,
∴![]() ,
,![]() ,
,
∵![]() ,
,
∴![]() ,
,
∴![]() ;
;
(2)作![]() 于
于![]() ,如图,则
,如图,则![]() ,设
,设![]() 的半径为
的半径为![]() ,
,
∵![]() ,
,
∴![]() ,
,
∴![]() ,即
,即![]() ,
,
解得![]() ,
,
∴![]() ,
,
∴![]() ,
,
在![]() 中,
中,![]() ,
,
∵![]() ,
,
而![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴![]() ,
,
整理得![]() ,
,
解得![]() (舍去),
(舍去),![]() ,
,
即![]() 的半径为
的半径为![]() .
.

练习册系列答案
相关题目