题目内容
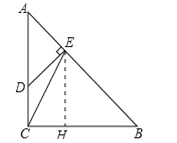
【题目】如图,在Rt△ABC中,∠ACB=90°,AC=BC=3,点D在边AC上,且AD=2CD,DE⊥AB,垂足为点E,联结CE,求:
(1)线段BE的长;
(2)∠ECB的余切值.

【答案】(1)![]() ;(2)
;(2)![]() .
.
【解析】
试题分析:(1)由等腰直角三角形的性质得出∠A=∠B=45°,由勾股定理求出AB,求出∠ADE=∠A=45°,由三角函数得出AE,即可得出BE的长;
(2)过点E作EH⊥BC,垂足为点H,由三角函数求出EH=BH=BEcos45°=2,得出CH=1,在Rt△CHE中,由三角函数求出cot∠ECB=![]() =
=![]() 即可.
即可.
试题解析:(1)∵AD=2CD,AC=3,∴AD=2,∵在Rt△ABC中,∠ACB=90°,AC=BC=3,∴∠A=∠B=45°,AB=![]() =
=![]() =
=![]() ,∵DE⊥AB,∴∠AED=90°,∠ADE=∠A=45°,∴AE=ADcos45°=
,∵DE⊥AB,∴∠AED=90°,∠ADE=∠A=45°,∴AE=ADcos45°=![]() =
=![]() ,∴BE=AB﹣AE=
,∴BE=AB﹣AE=![]() =
=![]() ,即线段BE的长为
,即线段BE的长为![]() ;
;
(2)过点E作EH⊥BC,垂足为点H,如图所示:
∵在Rt△BEH中,∠EHB=90°,∠B=45°,∴EH=BH=BEcos45°=![]() =2,∵BC=3,∴CH=1,在Rt△CHE中,cot∠ECB=
=2,∵BC=3,∴CH=1,在Rt△CHE中,cot∠ECB=![]() =
=![]() ,即∠ECB的余切值为
,即∠ECB的余切值为![]() .
.

练习册系列答案
相关题目