题目内容
【题目】如图,![]() 的直径
的直径![]() 为
为![]() ,弦
,弦![]() 为
为![]() ,
,![]() 、
、![]() 分别是
分别是![]() 的平分线与
的平分线与![]() ,
,![]() 的交点,
的交点,![]() 为
为![]() 延长线上一点,且
延长线上一点,且![]() .
.

![]() 求
求![]() 、
、![]() 的长;
的长;
![]() 试判断直线
试判断直线![]() 与
与![]() 的位置关系,并说明理由.
的位置关系,并说明理由.
【答案】(1)![]() ,
,![]() ;
;![]() 直线
直线![]() 与
与![]() 相切,理由详见解析.
相切,理由详见解析.
【解析】
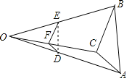
(1)连接BD,利用直径所对的圆周角是直角得两个直角三角形,再由角平分线得:∠ACD=∠DCB=45°,由同弧所对的圆周角相等可知:△ADB是等腰直角三角形,利用勾股定理可以求出直角边AD=5![]() ,AC的长也是利用勾股定理列式求得;
,AC的长也是利用勾股定理列式求得;
(2)连接半径OC,证明垂直即可;利用直角三角形中一直角边是斜边的一半得:这条直角边所对的锐角为30°,依次求得∠COB、∠CEP、∠PCE的度数,最后求得∠OCP=90°,结论得出.
解:(1)连接BD,
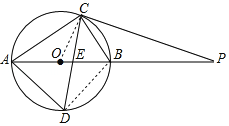
∵AB是⊙O的直径,
∴∠ACB=∠ADB=90°',
∵CD平分∠ACB,
∴∠ACD=∠DCB=45°,
∴∠ABD=∠ACD=45°,∠DAB=∠DCB=45°,
∴△ADB是等腰直角三角形,
∵AB=10,
∴AD=BD=![]() =5
=5![]() ,
,
在Rt△ACB中,AB=10,BC=5,
∴AC=![]() =5
=5![]() ,
,
∴![]() ,
,![]() ;
;
![]() 直线
直线![]() 与
与![]() 相切,理由是:
相切,理由是:
连接![]() ,
,
在![]() 中,
中,![]() ,
,![]() ,
,
∴![]() ,
,
∵![]() ,
,
∴![]() ,
,
∴![]() ,
,
∵![]() ,
,
∴![]() ,
,
∴![]() ,
,
∵![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴直线![]() 与
与![]() 相切.
相切.

练习册系列答案
 小学生10分钟口算测试100分系列答案
小学生10分钟口算测试100分系列答案
相关题目