题目内容
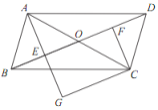
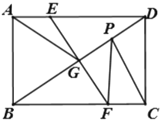
【题目】如图,在锐角等腰三角形ABC中,AB=AC,点O为△ABC外接圆的圆心,连结OC,过点B作AC的垂线,交⊙O于点D,交OC于点E,交AC于点F,连结AD和CD.
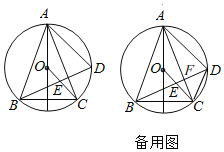
(1)若∠BAC=2α,则∠BDA= (用含α的代数式表示).
(2)①求证:OC∥AD;
②若E为OC的中点,求![]() 的值.
的值.
(3)若x=![]() ,y=
,y=![]() ,求y关于x的函数关系式.
,求y关于x的函数关系式.
【答案】(1)90°﹣α;(2)① 见解析;②![]() ;(3)y=2﹣
;(3)y=2﹣![]() .
.
【解析】
(1)由“在锐角等腰三角形ABC中,AB=AC,点O为△ABC外接圆的圆心”可知AG平分∠BAC,AG⊥BC,根据同弧所对的圆周角相等可得∠BDA=∠ BCA=![]() =90°﹣α;
=90°﹣α;
(2)①由(1)知∠OAC=α,∠ACB=90°﹣α,且BD⊥AC可Rt△ADF中推知∠CAD=∠OCA=α,即可证OC∥AD;
②由①知∠OAC=α=∠CAD,又BD⊥AC,可知AH=AD;设OH=a,在Rt△EFC和Rt△BGF中可证∠OEH=∠OHE=90°﹣α,从而证出OE=OH=a,加上E为OC的中点可得OA=OC=2a,AH=OA+OH=3a,![]() 的值即可求出;
的值即可求出;
(3)根据(1)所证,易证△BGH≌△CGM(ASA),从而HG=MG;设MG=m,⊙O的半径为r,则可表示出OG=r﹣m,AG=2r﹣m,AH=2r﹣2m,AD=AH=2r﹣2m,所以可得y=2﹣![]() ;由BD⊥AC,易证∠ACD=∠ABD=90°﹣2α,而∠COM=2∠CAM=2α,所以可知∠BCE=90°﹣2α,使∠BCE=∠ACD,又由(2)知,∠CBE=∠CAD=α,所以△ACD∽△BCE,
;由BD⊥AC,易证∠ACD=∠ABD=90°﹣2α,而∠COM=2∠CAM=2α,所以可知∠BCE=90°﹣2α,使∠BCE=∠ACD,又由(2)知,∠CBE=∠CAD=α,所以△ACD∽△BCE,![]() =
=![]() =
=![]() =x,再在Rt△ACG和Rt△COG中分别用勾股定理表示出CG ,整理可得
=x,再在Rt△ACG和Rt△COG中分别用勾股定理表示出CG ,整理可得![]() =
=![]() ,然后代入y=2﹣
,然后代入y=2﹣![]() ,即可求得y关于x的函数关系式.
,即可求得y关于x的函数关系式.
解:(1)记AO交BD于H,交BC于G,
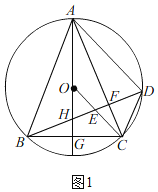
∵点O是等腰三角形△ABC的外接圆的圆心,
∴AG平分∠BAC,AG⊥BC,
∴∠CAG=![]() ∠BAC=α,
∠BAC=α,
∴∠ACB=90°﹣α,
∴∠BDA=∠ACB=90°﹣α,
故答案为:90°﹣α;
(2)①如图1,

由(1)知,∠OAC=α,
∵OA=OC,
∴∠OCA=∠OAC=α,
由(1)知,∠ACB=90°﹣α,
∵BD⊥AC,
∴∠BFC=90°,
∴∠CBF=90°﹣∠ACB=α,
∴∠CAD=∠CBF=α,
∴∠CAD=∠OCA=α,
∴OC∥AD;
②由①知,∠OAC=α=∠CAD,
∵BD⊥AC,
∴AH=AD,
设OH=a,
在Rt△EFC中,∠OCA=α,
∴∠OEH=∠CEF=90°﹣α,
在Rt△BGF中,∠CBF=α,
∴∠OHE=∠BHG=90°﹣α,
∴∠OEH=∠OHE,
∴OE=OH=a,
∵点E是OC的中点,
∴OC=2a,
∴OA=OC=2a,
∴AH=OA+OH=2a+a=3a,
∴![]() =
=![]() ;
;
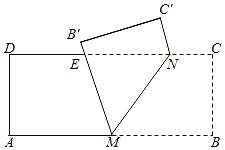
(3)如图2,
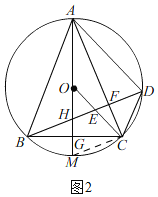
记AO与⊙O的另一个交点为M,连接CM,
由(1)知,∠CBD=∠BAG=α,
∵∠BCM=∠BAG=α,
∴∠CBD=∠BCM,
由(1)知,AG⊥BC,
∵AB=AC,
∴BG=CG,
∴△BGH≌△CGM(ASA),
∴HG=MG,
设MG=m,⊙O的半径为r,
∴OG=r﹣m,AG=2r﹣m,AH=2r﹣2m,
由(2)知,AD=AH=2r﹣2m,
∵y=![]() ,
,
∴y=![]() =2﹣
=2﹣![]() ①,
①,
∵BD⊥AC,
∴∠AFB=90°,
∴∠ABD=90°﹣∠BAC=90°﹣2α,
∴∠ACD=∠ABD=90°﹣2α,
∵∠COM=2∠CAM=2α,
∴∠BCE=90°﹣∠COM=90°﹣2α,
∴∠BCE=∠ACD,
由(2)知,∠CBE=∠CAD=α,
∴△ACD∽△BCE,
∴![]() =
=![]() =
=![]() ,
,
∵x=![]() ,
,
∴![]() =x,
=x,
∴AC2=4xCG2,
在Rt△ACG中,AG2=AC2﹣CG2=4xCG2﹣CG2=(4x﹣1)CG2,
∴CG=![]() =
=![]() ,
,
在Rt△COG中,CG=![]() =
=![]() ,
,
∴![]() =
=![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴![]() ﹣1=4x﹣1,
﹣1=4x﹣1,
∴![]() =
=![]() ②,
②,
将②代入①中,得y=2﹣2×![]() =2﹣
=2﹣![]() ,
,
即y关于x的函数关系式y=2﹣![]() .
.

【题目】2020年,新型冠状病毒肆虐全球,疫情期间学生在家进行网课学习和锻炼,学习和身体健康状况都有一定的影响.为了解学生身体健康状况,某校对学生进行立定跳远水平测试.随机抽取50名学生进行测试,并把测试成绩(单位:m)绘制成不完整的频数分布表和频数分布直方图.
学生立定跳远测试成绩的频数分布表
分组 | 频数 |
| a |
| 12 |
| b |
| 10 |
学生立定跳远测试成绩的频数分布直方图
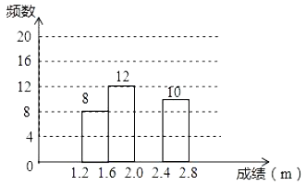
请根据图表中所提供的信息,完成下列问题:
(1)表中![]() ________,
________,![]() ________;
________;
(2)样本成绩的中位数落在________范围内;
(3)请把频数分布直方图补充完整;
(4)该校共有1200名学生,估计该学校学生立定跳远成绩在![]() 范围内的有多少人?
范围内的有多少人?
【题目】为了防范新冠肺炎疫情,某校在网络平台开展防疫宣传,并出了6道选择题,对甲、乙两个班级学生(各有40名学生)的答题情况进行统计分析,得到统计表如下:
答对的题数 | 0 | 1 | 2 | 3 | 4 | 5 | 6 |
甲班 | 0 | 2 | 3 | 4 | 17 | 12 | 2 |
乙班 | 0 | 1 | 5 | 3 | 15 | 14 | 2 |
请根据以上信息,解答下列问题:
(1)甲班学生答对的题数的众数为 ;
(2)若答对的题数大于或等于5道的为优秀,则乙班该次考试的优秀率为 ;
(3)从甲、乙两班答题全对的学生中随机抽取2人做学习防疫知识心得交流,通过画树状图或列表法,求抽到的2人来自同一个班级的概率.