题目内容
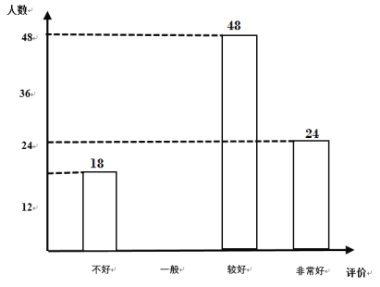
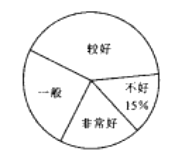
【题目】电子政务、数字经济、智慧社会……一场数字革命正在神州大地激荡,在第二届数字中国建设峰会召开之际,某校举行了第二届“掌握新技术,走进数时代”信息技术应用大赛,将该校八年级参加竞赛的学生成绩统计后,绘制成如下统计图表(不完整)
“掌握新技术,走进数时代”信息技术应用大赛成绩频数分布统计表:
组别 | 成绩x(分) | 人数 |
A | 60≤x<70 | 10 |
B | 70≤x<80 | m |
C | 80≤x<90 | 16 |
D | 90≤x≤100 | 4 |

请观察上面的图表,解答下列问题:
(1)统计表中m= ;统计图中n= ;B组的圆心角是 度.
(2)D组的4名学生中,有2名男生和2名女生.从D组随机抽取2名学生参加5G体验活动,请你画出树状图或用列表法求:
①恰好1名男生和1名女生被抽取参加5G体验活动的概率;
②至少1名女生被抽取参加5G体验活动的概率.
【答案】(1)20、32、144;(2)①![]() ;②
;②![]()
【解析】
(1)先根据A组人数及其所占百分比求出总人数,然后由各组人数之和等于总人数即可求出B组人数m的值,用C组人数除以总人数即可求出n的值,用360°乘以B组人数所占比百分比即可求出圆心角的度数;
(2)①列表得出所有等可能结果,从中找到恰好1名男生和1名女生被抽取参加5G体验活动的情况数,再利用所求情况数与总数之比求概率即可;
②从列表中找出至少1名女生被抽取参加5G体验活动的情况数,再利用所求情况数与总数之比求概率即可.
解:(1)被调查的总人数为10÷20%=50,
则m=50﹣(10+16+4)=20,
n%=![]() ×100%=32%,即n=32,
×100%=32%,即n=32,
B组的圆心角是360°×![]() =144°,
=144°,
故答案为:20、32、144;
(2)①设男同学标记为A、B;女学生标记为1、2,可能出现的所有结果列表如下:
A | B | 1 | 2 | |
A | / | (B,A) | (1,A) | (2,A) |
B | (A,B) | / | (1,B) | (2,B) |
1 | (A,1) | (B,1) | / | (2,1) |
2 | (A,2) | (B,2) | (1,2) | / |
共有 12 种可能的结果,且每种的可能性相同,其中刚好抽到一男一女的结果有8种,
∴恰好1名男生和1名女生被抽取参加5G体验活动的概率为![]() =
=![]() ;
;
②∵至少1名女生被抽取参加5G体验活动的有10种结果,
∴至少1名女生被抽取参加5G体验活动的概率为![]() =
=![]() .
.

 名校课堂系列答案
名校课堂系列答案【题目】寒假中,某校七年级开展“阅读经典,读一本好书”的活动.为了解学生阅读情况,从全年级学生中随机抽取了部分学生调查读书种类情况,并进行统计分析,绘制了如下不完整的统计图表:
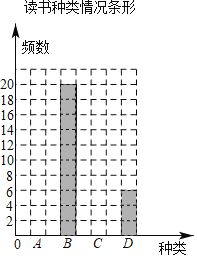
读书种类情况统计表
种类 | 频数 | 百分比 |
A.科普类 | a | 32% |
B.文学类 | 20 | 40% |
C.艺术类 | 8 | b |
D.其他类 | 6 | 12% |
请根据以上信息,解答下列问题:
(1)填空:a= ,b= ,并补全条形统计图;
(2)若绘制“阅读情况扇形统计图”,则“艺术类”所对应扇形的圆心角度数为 °;
(3)若该校七年级共有800人,请估计全年级在本次活动中读书种类为“艺术类”的学生人数.