题目内容
【题目】抛物线y=﹣x2+bx+c与x轴交于A、B两点(点A在B左边),与y轴交于点C.
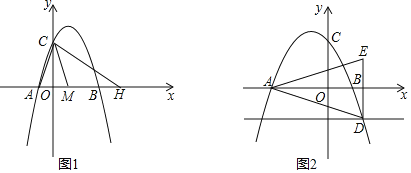
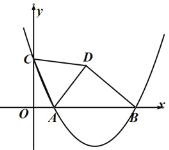
(1)如图1,已知A(﹣1,0),B(3,0).
①直接写出抛物线的解析式;
②点H在x轴上,M(1,0),连接AC、MC、HC,若CM平分∠ACH,求H的坐标;
(2)如图2,直线y=﹣1与抛物线y=﹣x2+bx+c交于抛物线对称轴右侧的点为点D,点E与点D关于x轴对称.试判断直线DB与直线AE的位置关系,并证明你的结论.
【答案】(1)①y=﹣x2+2x+3,②(![]() ,0);(2)DB⊥AE,见解析
,0);(2)DB⊥AE,见解析
【解析】
(1)①用待定系数法解答便可;
②过H作HN∥AC与CM的延长线交于点N,证明△ACM∽△HNM,进而得![]() ,再在△OCH中,由勾股定理得列出方程便可求得结果;
,再在△OCH中,由勾股定理得列出方程便可求得结果;
(2)设DE与x轴交于点K,先求出D点坐标,进而得BK、DK、EK、AK,再计算tan∠BDK和tan∠EAK,得这两角相等,最后推理得∠BDK+∠E=90°便可.
(1)①把A(﹣1,0),B(3,0)代入y=﹣x2+bx+c中,得
![]() ,
,
∴![]() ,
,
∴抛物线的解析式为y=﹣x2+2x+3;
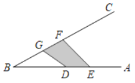
②过H作HN∥AC与CM的延长线交于点N,如图1
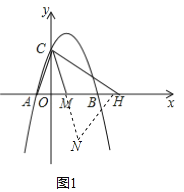
∴△ACM∽△HNM,
∴![]() ,
,
∴∠ACN=∠N,
∵CM平分∠ACH,
∴∠HCN=∠ACN=∠CNH,
∴CH=NH,
∴![]() ,
,
∵C(0,3),
∴![]() ,
,
AM=2,
∴![]() ,
,
∴![]() ,
,
设MH=2a,则CH=![]() a,
a,
∵OC2+OH2=CH2,
∴![]() ,
,
解得,a=﹣1(舍去),或![]() ,
,
∴![]() ,
,
∴H(![]() ,0);
,0);
(2)当y=﹣1时,y=﹣x2+bx+c=﹣1,则x2﹣bx﹣c﹣1=0,
∴![]() ,
,
∴D(![]() ,﹣1),
,﹣1),
当y=0时,y=﹣x2+bx+c=0,即x2﹣bx﹣c=0,则![]() ,
,
∴![]() ,
,![]() ,
,
设DE与x轴交于点K,
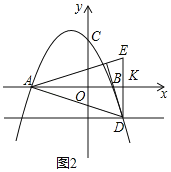
则![]() ,
,
∴![]() ,
,
又![]() ,
,
∴ ,
,
∴∠BDK=∠EAK,
∵DE⊥AK,
∴∠EAK+∠E=90°,
∴∠BDK+∠E=90°,
∴BD⊥AE.

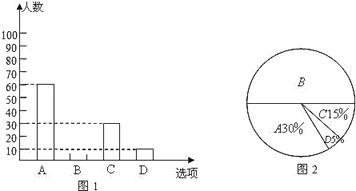
【题目】电子政务、数字经济、智慧社会……一场数字革命正在神州大地激荡,在第二届数字中国建设峰会召开之际,某校举行了第二届“掌握新技术,走进数时代”信息技术应用大赛,将该校八年级参加竞赛的学生成绩统计后,绘制成如下统计图表(不完整)
“掌握新技术,走进数时代”信息技术应用大赛成绩频数分布统计表:
组别 | 成绩x(分) | 人数 |
A | 60≤x<70 | 10 |
B | 70≤x<80 | m |
C | 80≤x<90 | 16 |
D | 90≤x≤100 | 4 |

请观察上面的图表,解答下列问题:
(1)统计表中m= ;统计图中n= ;B组的圆心角是 度.
(2)D组的4名学生中,有2名男生和2名女生.从D组随机抽取2名学生参加5G体验活动,请你画出树状图或用列表法求:
①恰好1名男生和1名女生被抽取参加5G体验活动的概率;
②至少1名女生被抽取参加5G体验活动的概率.