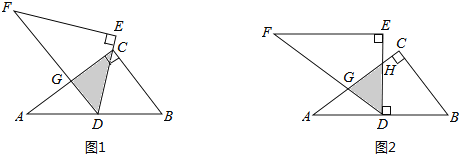题目内容
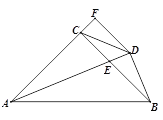
【题目】如图,在△ABC中,AC=BC,∠ ACB=90°,AE平分∠BAC交BC于E,BD⊥AE于D,DF⊥AC交AC的延长线于F,连接CD,给出四个结论:①∠ADC=45°;②BD=![]() AE;③AC+CE=AB;④AB—BC=2FC;其中正确的结论有( )
AE;③AC+CE=AB;④AB—BC=2FC;其中正确的结论有( )
A. 1个 B. 2个 C. 3个 D. 4个
【答案】D
【解析】试题分析:过点E作EQ⊥AB于Q,∵∠ACB=90°,AE平分∠CAB,∴CE=EQ,∵∠ACB=90°,AC=BC ∴∠CBA=∠CAB=45° ∵EQ⊥AB ∴∠EQA=∠EQB=90° 由勾股定理可得AC=AQ ∴∠QEB=45°=∠CBA
∴EQ=BQ ∴AB=AQ+BQ=AC+CE ∴③正确
作∠ACN=∠BCD,交AD于N,∵∠CAD=![]() ∠CAB=22.5°=∠BAD ∴∠ABD=67.5° ∴∠DBC=22.5°=∠CAD
∠CAB=22.5°=∠BAD ∴∠ABD=67.5° ∴∠DBC=22.5°=∠CAD
∴∠DBC=∠CAD ∵AC=BC ∠ACN=∠DCB ∴△ACN≌△BCD ∴CN=CD AN=BD ∵∠ACN+∠NCE=90°
∴∠NCB+∠BCD=90° ∴∠CND=∠CDA=45° ∴∠ACN=22.5°=∠CAN ∴AN=CN ∴∠NCE=∠AEC=67.5°
∴CN=NE ∴CD-AN=EN=![]() AE ∵AN=BD ∴BD=
AE ∵AN=BD ∴BD=![]() AE ∴①正确 ②正确.
AE ∴①正确 ②正确.
过D作DH⊥AB于H,∵∠FCD=∠CAD+∠CDA=67.5° ∠DBA=90°-∠DAB=67.5° ∴∠FCD=∠DBA
∵AE平分∠CAB DF⊥AC,DH⊥AB,∴DF=DH ∴△DCF≌△DBH ∴BH=CF 由勾股定理可得:AF=AH
∴![]() ,∴AC+AB=2AF AC+AB=2AC+2CF
,∴AC+AB=2AF AC+AB=2AC+2CF
AB-AC=2CF ∵AC=CB ∴AB-CB=2CF ∴④正确.

练习册系列答案
相关题目