题目内容
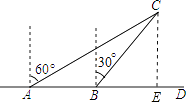
【题目】如图,一艘轮船在A处时观测得小岛C在船的北偏东60°方向,轮船以40海里/时的速度向正东方向航行1.5小时到达B处,这时小岛C在船的北偏东30°方向.已知小岛C周围50海里范围内是暗礁区.
(1)求B处到小岛C的距离
(2)若轮船从B处继续向东方向航行,有无触礁危险?请说明理由.
(参考数据: ![]() ≈1.73)
≈1.73)
【答案】
(1)
解:由题意得∠CBD=60°,∠CAB=30°,
∴∠ACB=30°,
∴∠CAB=∠ACB,
∴CB=AB=40×1.5=60(海里),
∴B处到小岛C的距离为60海里
(2)
解:过点C作CE⊥AD,垂足为点E,
∵CE=CB×sin∠CBE=60×sin60°=30 ![]() ≈51.96海里,
≈51.96海里,
∴CE>50,
∴轮船从B处继续向正东方向航行,没有触礁危险.
【解析】(1)先证明∠CAB=∠ACB,可得CB=AB,再根据路程=速度×时间就是健康求解;(2)过点C作CE⊥AD,垂足为点E,根据锐角三角函数的概念求出CE,与50海里比较即可.
【考点精析】本题主要考查了关于方向角问题的相关知识点,需要掌握指北或指南方向线与目标方向 线所成的小于90°的水平角,叫做方向角才能正确解答此题.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目



