��Ŀ����
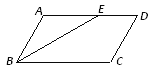
����Ŀ����ͼ������������������A��B��C������������⣺
![]()
(1)����B�����ƶ�������λ���ȵ���D���������ϱ�ʾ����D��
(2)���������ҵ���E��ʹ��EΪBA���е㣨E��A��C����ľ�����ȣ������������ϱ����E��ʾ���������CE�ij���
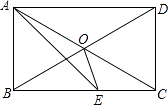
(3)OΪԭ�㣬ȡOC���е�M����OC��Ϊ���Σ���Ϊ��һ�β�����ȡ������OM��CM���е�ֱ�Ϊ��N1��N2����OC��Ϊ4�Σ���Ϊ�ڶ��β�������ȡ�����ε��е㽫OC��Ϊ8�Σ���Ϊ�����β����������β�����OC֮�乲�ж��ٸ��㣿�����Щ������ʾ�����ĺͣ�
���𰸡���1����ͼ��ʾ����������2����ͼ��ʾ����E��ʾ����Ϊ����3.5��CE=4������3.5��=7.5����3��OC֮�乲��65���㣻��Щ������ʾ�����ĺ�Ϊ130��
��������
��1�����������ϵĵ��ƶ�ʱ�Ĵ�С�仯���ɣ���������Ҽ������ɵõ����ۣ�
��2������������ʽ���㼴�ɣ�
��3����������õ�������2��ָ������+1���ݴ˼��㼴�ɣ�
��1����ͼ��ʾ��
![]()
��2����ͼ��ʾ����E��ʾ����Ϊ����3.5��
�ߵ�C��ʾ����Ϊ��4��
��CE=4������3.5��=7.5��
��3���ߵ�һ�β�������3=��21+1�����㣬
�ڶ��β�������5=��22+1�����㣬
�����β�������9=��23+1�����㣬
������β�����OC֮�乲�У�26+1��=65���㣻
��65�����ȥ0��64������
����Щ������ʾ�����ĺ�=4����![]() ��=130��
��=130��

����Ŀ��Ϊ�˽�һ���ռ�����֪ʶ�����������Ļ������о����ˡ������У��֪ʶ�������Ϊ�˽�����֪ʶ���ռ�����������ȡ�˲��ֻ���������������õ����в�������ͳ��ͼ����
�ȴ� | Ƶ�� | Ƶ�� |
һ�Ƚ� | 10 | 0.05 |
���Ƚ� | 20 | 0.10 |
���Ƚ� | 30 | b |
��ʤ�� | a | 0.30 |
������ | 80 | 0.40 |
�����������Ϣ������������⣺
��1��a= �� b= �� �Ҳ�ȫƵ���ֲ�ֱ��ͼ��
��2����������ͳ��ͼ�������ֲ�������ʻ����ʤ����Ӧ������Բ�ĽǵĶ����Ƕ��٣�
��3�������г���������16000�ˣ����������Ϊ40%�������Ƚ����ϵ�ѧ����ʾ�ԡ�����Ƚ�ϲ����������������г������ԡ�����Ƚ�ϲ�������ж����ˣ�