题目内容
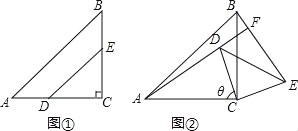
【题目】如图①,在△ABC中,∠ACB=90°,AC=BC,在AC、BC边上分别截取CD=CE,连结DE.将△DCE绕着点C顺时针旋转θ角,连结BE、AD.
(1)当0°<θ<90°时,如图②,直线BE交直线AD于点F.
①求证:△ACD≌△BCE.
②求证:AF⊥BE.
(2)当0°<θ<360°,AC=5,CD=3,四边形CDFE是正方形时,直接写出AF的长度.
【答案】(1)证明见解析;(2)1.
【解析】
试题分析: (1)①根据旋转的性质和已知,运用SAS证明即可;②由问题原型中的结论:△ACE≌△BCE得出∠BFO=∠ACB,结合等量代换进行求解即可;
(2)运用CD∥BE结合初步探究中的结论,可证CD⊥AF,结合勾股定理即可求解.
试题解析:(1)①如图②,
∵△DCE绕着点C顺时针旋转θ角,由旋转的性质可知,
∴∠ACD=∠BCE=θ,
又∵AC=BC,CD=CE,
在△ACD和△BCE中,
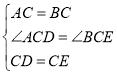 ,
,
∴△ACD≌△BCE;
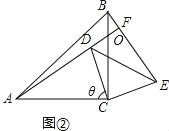
②如图②,设AF与BC交点于O,
∵△ACD≌△BCE,
∴∠DAC=∠EBC,
∵∠AOC=∠BOF,
∴∠BFO=∠ACB=90°,
∴AF⊥BE;
(2)如图③,
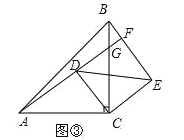
∵AC=5,CD=3,四边形CDFE是正方形时,
∵AD⊥CD,
∴AD=![]() ,
,
∴AF=4+3=7,
如图4,
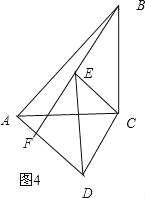
∴AF=4﹣3=1.

练习册系列答案
相关题目