题目内容
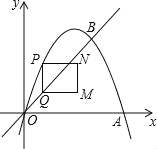
【题目】如图,在平面直角坐标系中,抛物线y=ax2+bx与x轴交于O、A两点,与直线y=x交于点B,点A、B的坐标分别为(3,0)、(2,2).点P在抛物线上,过点P作y轴的平行线交射线OB于点Q,以PQ为边向右作矩形PQMN,且PN=1,设点P的横坐标为m(m>0,且m≠2).
(1)求这条抛物线所对应的函数表达式.
(2)求矩形PQMN的周长C与m之间的函数关系式.
(3)当矩形PQMN是正方形时,求m的值.
【答案】(1)y=﹣x2+3x.(2)①当0<m<2时,C=﹣2m2+4m+2.②当m>2时,C=2m2﹣4m+2.(3)1或1+![]() .
.
【解析】
试题分析: (1)把A(3,0)、B(2,2)两点坐标代入y=ax2+bx,解方程组即可解决.
(2)分两种情形:①0<m<2,②m>2,分别求出矩形PQMN的周长C与m之间的函数关系式即可.
(3)分两种情形列出方程即可解决.
试题解析:(1)把A(3,0)、B(2,2)两点坐标代入y=ax2+bx,
得![]() ,解得
,解得![]() .
.
故抛物线所对应的函数表达式为y=﹣x2+3x.
(2)∵点P在抛物线y=﹣x2+3x上,
∴可以设P(m,﹣m2+3m),
∵PQ∥y轴,
∴Q(m,m).
①当0<m<2时,如图1中,

PQ=﹣m2+3m﹣m=﹣m2﹣2m,
C=2(﹣m2+2m)+2=﹣2m2+4m+2.
②当m>2时,如图2中,

PQ=m﹣(﹣m2+3m)=m2﹣2m,
C=2(m2﹣2m)+2=2m2﹣4m+2.
(3)∵矩形PQMN是正方形,
∴PQ=PN=1,
当0<m<2时,如图3中,

﹣m2+2m=1,解得m=1.
当m>2时,如图4中,

m2﹣2m=1,解得m=1+![]() (或1﹣
(或1﹣![]() 不合题意舍弃).
不合题意舍弃).

练习册系列答案
相关题目