Question

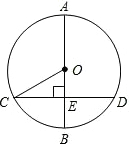
如图，隧道的截面由圆弧AED和矩形ABCD构成，矩形的长BC为12m，宽AB为3m，隧道的顶端E（圆弧AED的中点）高出道路（BC）7m．
（1）求圆弧AED所在圆的半径；
（2）如果该隧道内设双行道，现有一辆超高货运卡车高6.5m，宽2.3m，问这辆货运卡车能否通过该隧道．

Answer 1

（1）设圆心为点O，半径为R，连接OE交AD于F点，连接OA，OD，
由垂径定理，得OF垂直平分AD，AF=6，OF=R-（7-3）=R-4，
由勾股定理，得AF²+OF²=OA²，即：6²+（R-4）²=R²，
解得R=6.5米；

（2）能通过，但要小心．
车宽GH=2.3，圆的半径OH=6.5，
由勾股定理，得OG=

6.52-2.32

≈6.08，
G点与BC的距离为7-6.5+6.08=6.58＞6.5；能通过．