题目内容
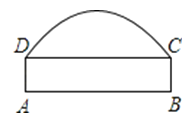
【题目】如图,有一条双向公路隧道,其横断面由抛物线和矩形ABCD的三边DA、AB、BC围成,隧道最大高度为4.9米,AB=10米,BC=2.4米,若有一辆高为4米、宽为2米的集装箱的汽车要通过隧道,为了使箱顶不碰到隧道顶部,又不违反交通规则(汽车应靠道路右侧行驶,不能超过道路中线),汽车的右侧必须离开隧道右壁几米?
【答案】2米.
【解析】
以AB为x轴,其中点为坐标原点建立平面直角坐标系,则B点坐标为(5,0),E点坐标为(0,4.9),C点坐标为(5,2.4),求得抛物线解析式,进一步利用图象上的点解答即可.
如图,建立平面直角坐标系,
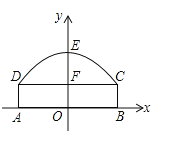
由题意知,B点坐标为(5,0),E点坐标为(0,4.9),C点坐标为(5,2.4),
设抛物线解析式为y=ax2+4.9,代入C点
解得a=﹣0.1,
因此抛物线解析式为y=﹣0.1x2+4.9;
当汽车高4米,代入抛物线的解析式y=﹣0.1x2+4.9,
解得x=±3(舍去负值),
∴x=3,
5﹣3=2,
即车右侧到中线的水平距离为3米.则汽车的右侧离开隧道右壁2米才不至于碰到隧道顶部.
答:汽车的右侧离开隧道右壁2米才不至于碰到隧道顶部.

练习册系列答案
相关题目
【题目】一个批发商销售成本为20元/千克的某产品,根据物价部门规定:该产品每千克售价不得超过90元,在销售过程中发现的售量y(千克)与售价x(元/千克)满足一次函数关系,对应关系如下表:
售价x(元/千克) | … | 50 | 60 | 70 | 80 | … |
销售量y(千克) | … | 100 | 90 | 80 | 70 | … |
(1)求y与x的函数关系式;
(2)该批发商若想获得4000元的利润,应将售价定为多少元?
(3)该产品每千克售价为多少元时,批发商获得的利润w(元)最大?此时的最大利润为多少元?