Question

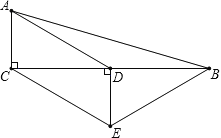
【题目】如图1，在△ABC和△ADE中，∠BAC＝∠EAD，AB＝AC，AD＝AE，连接CD、AE交于点F．

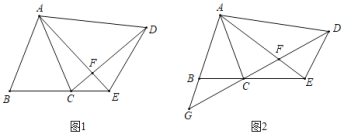
（1）求证：BE＝CD．

（2）当∠BAC＝∠EAD＝30°，AD⊥AB时（如图2），延长DC、AB交于点G，请直接写出图中除△ABC、△ADE以外的等腰三角形．

Answer 1

【答案】（1）见解析；（2）△ACF是等腰三角形，△ADG是等腰三角形，△DEF是等腰三角形，△ECD是等腰三角形．

【解析】

（1）由“SAS”可证△ACD≌△ABE，可得BE＝CD；

（2）如图2，图形中有四个等腰三角形：分别是①△ACF是等腰三角形，②△ADG是等腰三角形，③△DEF是等腰三角形；④△ECD是等腰三角形；根据已知角的度数依次计算各角的度数，根据两个角相等的三角形是等腰三角形得出结论．

解：（1）如图1，∵∠BAC＝∠EAD，

∴∠BAC+∠CAE＝∠EAD+∠CAE，

即∠BAE＝∠CAD，且AB＝AC，AD＝AE，

∴△ACD≌△ABE（SAS）

∴BE＝CD；

（2）如图2，

①∵∠BAC＝∠EAD＝30°，

∴∠ABC＝∠ACB＝∠AED＝∠ADE＝75°，

由（1）得：∠ACD＝∠ABC＝75°，

∠DCE＝∠BAC＝30°，

∵AD⊥AB，

∴∠BAD＝90°，

∴∠CAE＝30°，

∴∠AFC＝180°﹣30°﹣75°＝75°，

∴∠ACF＝∠AFC，

∴△ACF是等腰三角形，

②∵∠BCG＝∠DCE＝30°，∠ABC＝75°，

∴∠G＝45°，

在Rt△AGD中，∠ADG＝45°，

∴△ADG是等腰三角形，

③∠EDF＝75°﹣45°＝30°，

∴∠DEF＝∠DFE＝75°，

∴△DEF是等腰三角形；

④∵∠ECD＝∠EDC＝30°，

∴△ECD是等腰三角形．