Question

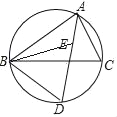
【题目】如图，在等边中，点在边上，过点且分别与边、相交于点、、是上的点，判断下列说法错误的是（ ）

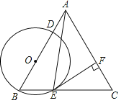
A. 若，则是的切线 B. 若是的切线，则

C. 若，则是的切线 D. 若，则是的切线

Answer 1

【答案】C

【解析】

如图1，连接OE，根据同圆的半径相等得到OB=OE，根据等边三角形的性质得到∠BOE=∠BAC，求得OE∥AC，于是得到A选项正确；B、由于EF是⊙O的切线，得到OE⊥EF，根据平行线的性质得到B选项正确；C、根据等边三角形的性质和圆的性质得到AO=OB，如图2，过O作OH⊥AC于H，根据三角函数得到OH=AO≠OB，于是得到C选项错误；D、如图2，根据等边三角形的性质和等量代换即可得到D选项正确．

A、如图1，连接OE，

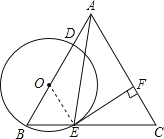
则OB=OE，

∵∠B=60°

∴∠BOE=60°，

∵∠BAC=60°，

∴∠BOE=∠BAC，

∴OE∥AC，

∵EF⊥AC，

∴OE⊥EF，

∴EF是⊙O的切线，

∴A选项正确；

B、∵EF是⊙O的切线，

∴OE⊥EF，

由A知：OE∥AC，

∴AC⊥EF，

∴B选项正确；

C、∵∠B=60°，OB=OE，

∴BE=OB，

∵BE=CE，

∴BC=AB=2BO，

∴AO=OB，

如图2，过O作OH⊥AC于H，

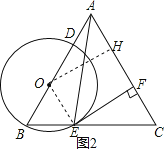
∵∠BAC=60°，

∴OH=AO≠OB，

∴C选项错误；

D、如图2，∵BE=EC，

∴CE=BE，

∵AB=BC，BO=BE，

∴AO=CE=OB，

∴OH=AO=OB，

∴AC是⊙O的切线，

∴D选项正确．

故选C．