Question

【题目】直角△ABC中，∠C=90°，点D，E分别是边AC，BC上的点，点P是一动点．令∠PDA=∠1，∠PEB=∠2，∠DPE=∠α．

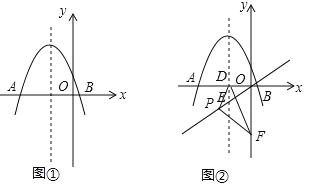
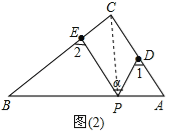
（1）若点P在线段AB上，如图①，且∠α=50°，则∠1+∠2=　　　　　　；

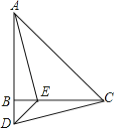
（2）若点P在斜边AB上运动，如图②，则∠α、∠1、∠2之间的关系为　　　　　　；

（3）如图③，若点P在斜边BA的延长线上运动（CE＜CD），请直接写出∠α、∠1、∠2之间的关系：　　　　　　；

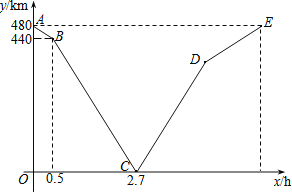
（4）若点P运动到△ABC形外（只需研究图④情形），则∠α、∠1、∠2之间有何关系？并说明理由．

Answer 1

【答案】（1）140°（2）∠1+∠2=90°+∠α（3）∠2﹣∠1=90°+∠α；∠2=∠1+90°；∠1﹣∠2=∠α﹣90°（4）∠2=90°+∠1﹣α，理由见解析

【解析】试题分析:（1）连接PC，根据三角形的一个外角等于与它不相邻的两个内角的和可得∠1=∠PCD+∠CPD，∠2=∠PCE+∠CPE，再表示出∠1+∠2即可；

（2）利用（1）中所求得出答案即可；

（3）利用三角外角的性质分三种情况讨论即可；

（4）利用三角形内角和定理以及邻补角的性质可得出．

解：（1）如图，连接PC，

∵∠1=∠PCD+∠CPD，∠2=∠PCE+∠CPE，

∴∠1+∠2=∠PCD+∠CPD+∠PCE+∠CPE=∠DPE+∠C，

∵∠DPE=∠α=50°，∠C=90°，

∴∠1+∠2=50°+90°=140°，

故答案为：140°；

（2）连接PC，

∵∠1=∠PCD+∠CPD，∠2=∠PCE+∠CPE，

∴∠1+∠2=∠PCD+∠CPD+∠PCE+∠CPE=∠DPE+∠C，

∵∠C=90°，∠DPE=∠α，

∴∠1+∠2=90°+∠α；

故答案为：∠1+∠2=90°+∠α；

（3）如图1，

∵∠2=∠C+∠1+∠α，

∴∠2﹣∠1=90°+∠α；

如图2，∠α=0°，∠2=∠1+90°；

如图3，∵∠2=∠1﹣∠α+∠C，

∴∠1﹣∠2=∠α﹣90°．

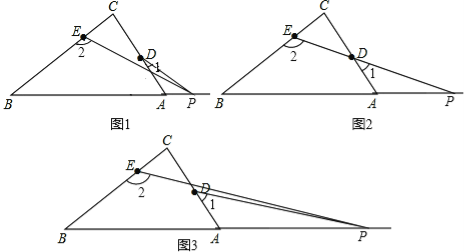
故答案为；∠2﹣∠1=90°+∠α；∠2=∠1+90°；∠1﹣∠2=∠α﹣90°．

（4）

∵∠PFD=∠EFC，

∴180°﹣∠PFD=180°﹣∠EFC，

∴∠α+180°﹣∠1=∠C+180°﹣∠2，

∴∠2=90°+∠1﹣α．

故答案为：∠2=90°+∠1﹣α．