题目内容
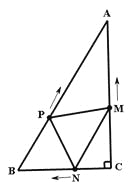
【题目】如图,在RtΔABC中,∠C=90,AC=4cm,BC=3cm.动点M、N从点C同时出发,均以每秒1cm的速度分别沿CA、CB向终点A、B移动,同时动点P从点B出发,以每秒2cm的速度沿BA向终点A移动。连接PM、PN。设移动时间为t(单位:秒,0<t<2.5).
(1)当t为何值时,以A、P、M为顶点的三角形与ΔABC相似?
(2)是否存在某一时刻t,使△PMN 的面积恰好是△ABC 面积的![]() ;若存在求t的值;若不存在,请说明理由.
;若存在求t的值;若不存在,请说明理由.

【答案】(1)、t=![]() ;(2)、t=
;(2)、t=![]()
【解析】试题分析:(1)、分ΔAMP∽ΔABC和ΔAPM∽ΔABC两种情况讨论;(2)、用t表示出各边长和△PMN 的面积,根据△PMN 的面积恰好是△ABC 面积的![]() 得出一元二次方程,然后解方程即可.
得出一元二次方程,然后解方程即可.
试题解析:(1)、由以A、P、M为顶点的三角形与ΔABC相似,分两种情况:
若ΔAMP∽ΔABC, 则![]() ∴
∴![]()
![]() ∴t=
∴t=![]() ,
,
若ΔAPM∽ΔABC, 则![]() ∴
∴![]() , ∴t=0(不合题意,舍去)
, ∴t=0(不合题意,舍去)
当t=![]() 时,以A、P、M为顶点的三角形与ΔABC相似.
时,以A、P、M为顶点的三角形与ΔABC相似.
(2)、![]()
![]()
![]() (舍去)
(舍去)![]()

 能力评价系列答案
能力评价系列答案 唐印文化课时测评系列答案
唐印文化课时测评系列答案 导学与测试系列答案
导学与测试系列答案【题目】某天,一蔬菜经营户用60元钱从蔬菜批发市场批了西红柿和豆角共40㎏到菜市场去卖,西红柿和豆角这天的批发价与零售价如下表所示:问:他当天卖完这些西红柿和豆角能赚多少钱?
品名 | 西红柿 | 豆角 |
批发价(单位:元/kg) | 1.2 | 1.6 |
零售价(单位:元/kg) | 1.8 | 2.5 |
【题目】某学校要成立一支由6名女生组成的礼仪队,八年级两个班各选6名女生,分别组成甲队和乙队参加选拔.每位女生的身高统计如图,部分统计量如下表:
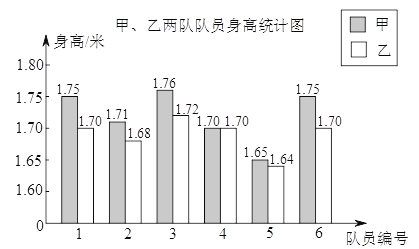
平均数 | 标准差 | 中位数 | |
甲队 | 1.72 | 0.038 | |
乙队 | 0.025 | 1.70 |
(1)求甲队身高的中位数;
(2)求乙队身高的平均数及身高不小于1.70米的频率;
(3)如果选拔的标准是身高越整齐越好,那么甲、乙两队
中哪一队将被录取?请说明理由.