题目内容
在⊙O中,直径为10,AB是弦,且AB=8,则圆心O与弦AB的距离为______.
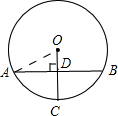
过⊙O的圆心O作OC⊥AB于点D.连接OA.
则AD=BD=
AB(垂径定理).
又∵AB=8,
∴AD=4;
∵⊙O的直径为10,
∴OA=5(圆的半径是直径的一半);
在Rt△AOD中,OD=
=3(勾股定理).
故答案是:3.
则AD=BD=
| 1 |
| 2 |
又∵AB=8,
∴AD=4;
∵⊙O的直径为10,
∴OA=5(圆的半径是直径的一半);
在Rt△AOD中,OD=
| OA2-AD2 |
故答案是:3.


练习册系列答案
 开心快乐假期作业暑假作业西安出版社系列答案
开心快乐假期作业暑假作业西安出版社系列答案
相关题目