题目内容
如图,BC是⊙O的直径,点A在圆上,且AB=AC=4.P为AB上一点,过P作PE⊥AB分别交BC、OA于E、F.
(1)设AP=1,求△OEF的面积;
(2)设AP=a(0<a<2),△APF、△OEF的面积分别记为S1、S2.
①若S1=S2,求a的值;
②若S=S1+S2,是否存在一个实数a,使S<
?若存在,求出一个a的值;若不存在,说明理由.
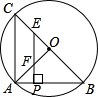
(1)设AP=1,求△OEF的面积;
(2)设AP=a(0<a<2),△APF、△OEF的面积分别记为S1、S2.
①若S1=S2,求a的值;
②若S=S1+S2,是否存在一个实数a,使S<
| ||
| 3 |

(1)∵BC是⊙O的直径,
∴∠BAC=90°,
∵AB=AC
∴∠B=∠C=45°,OA⊥BC,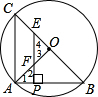
∴∠1=∠B=45°,
∵PE⊥AB
∴∠2=∠1=45°
∴∠4=∠3=45°,
则△APF、△OEF与△OAB均为等腰直角三角形.
∵AP=l,AB=4,
∴AF=
,OA=2
,
∴OE=OF=
,
∴△OEF的面积为
•OE•OF=1.
(2)①∵FP=AP=a,
∴S1=
a2
且AF=
a,
∴OE=OF=2
-
a=
(2-a),
∴S2=
•OE•OF=(2-a)2
∵S1=S2
∴
a2=(2-a)2
∴a=4±2
∵0<a<2
∴a=4-2
.
②S=S1+S2=
a2+(2-a)2=
a2-4a+4=
(a-
)2+
,
∴当a=
时,S取得最小值为
,
∵
<
,
∴不存在这样实数a,使S<
.
∴∠BAC=90°,
∵AB=AC
∴∠B=∠C=45°,OA⊥BC,

∴∠1=∠B=45°,
∵PE⊥AB
∴∠2=∠1=45°
∴∠4=∠3=45°,
则△APF、△OEF与△OAB均为等腰直角三角形.
∵AP=l,AB=4,
∴AF=
| 2 |
| 2 |
∴OE=OF=
| 2 |
∴△OEF的面积为
| 1 |
| 2 |
(2)①∵FP=AP=a,
∴S1=
| 1 |
| 2 |
且AF=
| 2 |
∴OE=OF=2
| 2 |
| 2 |
| 2 |
∴S2=
| 1 |
| 2 |
∵S1=S2
∴
| 1 |
| 2 |
∴a=4±2
| 2 |
∵0<a<2
∴a=4-2
| 2 |
②S=S1+S2=
| 1 |
| 2 |
| 3 |
| 2 |
| 3 |
| 2 |
| 4 |
| 3 |
| 4 |
| 3 |
∴当a=
| 4 |
| 3 |
| 4 |
| 3 |
∵
| ||
| 3 |
| 4 |
| 3 |
∴不存在这样实数a,使S<
| ||
| 3 |

练习册系列答案
 综合自测系列答案
综合自测系列答案
相关题目
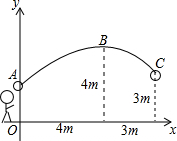 中心的水平距离为7米,当球出手后水平距离为4米时到达最大高度4米,设篮球运行路线为抛物线,篮圈距地面3米.
中心的水平距离为7米,当球出手后水平距离为4米时到达最大高度4米,设篮球运行路线为抛物线,篮圈距地面3米.