题目内容
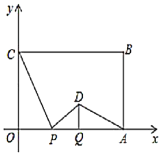
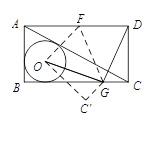
【题目】如图,已知矩形ABCD,⊙O是△ABC的内切圆,现将矩形ABCD按如图所示折叠,使点D与点O重合,折痕为FG,点F、G分别在AD,BC上,连接OG、DG,若OG⊥DG,且⊙O的半径长为1,则下列结论不成立的是
A.CD+DF=4B.CDDF=2![]() 3
3
C.BC+AB=2![]() +4D.BCAB=2
+4D.BCAB=2
【答案】A
【解析】
设⊙O与BC的切点为M,如图1,连接MO并延长MO交AD于点N,可证明△OMG≌△GCD,得到OM=GC=1,CD=GM=BC-BM-GC=BC-2,设AB=a,BC=b,AC=c,则根据切线长的性质,由图2可知![]() =1,即c=a+b-2,根据勾股定理可求得a=
=1,即c=a+b-2,根据勾股定理可求得a=![]() ,或a=
,或a=![]() (舍去),因此可求出AB=
(舍去),因此可求出AB=![]() ,BC=
,BC=![]() ,所以BC-AB=2,BC+AB=
,所以BC-AB=2,BC+AB=![]() ;如图3,,设DF=x,则在Rt△ONF中,FN=3+
;如图3,,设DF=x,则在Rt△ONF中,FN=3+![]() -1-x,OF=x,ON=1+
-1-x,OF=x,ON=1+![]() -1=
-1=![]() ,由勾股定理得x=4-
,由勾股定理得x=4-![]() ,从而求得CD-DF=
,从而求得CD-DF=![]() ,CD+DF=5即可得出答案.
,CD+DF=5即可得出答案.
解:如图,
设⊙O与BC的切点为M,连接MO并延长MO交AD于点N,
∵将矩形ABCD按如图所示的方式折叠,使点D与点O重合,折痕为FG,
∴OG=DG,
∵OG⊥DG,
∴∠MGO+∠DGC=90°,
∵∠MOG+∠MGO=90°,
∴∠MOG=∠DGC,
在△OMG和△GCD中,
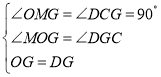
∴△OMG≌△GCD,
∴OM=GC=1,CD=GM=BC-BM-GC=BC-2.
∵AB=CD,
∴BC-AB=2.
设AB=a,BC=b,AC=c,⊙O的半径为r,
⊙O是Rt△ABC的内切圆可得r=![]() (a+b-c),
(a+b-c),
∴c=a+b-2.
在Rt△ABC中,由勾股定理可得a2+b2=(a+b-2)2,
整理得2ab-4a-4b+4=0,
又∵BC-AB=2即b=2+a,代入可得2a(2+a)-4a-4(2+a)+4=0,
解得:![]() (舍去),
(舍去),
![]()
![]()
再设DF=x,在Rt△ONF中, ![]()
由勾股定理可得![]()
解得![]()
![]()
综上只有选项A错误,
故选:A.