��Ŀ����
����Ŀ����ͼ����ƽ��ֱ������ϵ�У�ֱ��������AOB�Ķ���A��B�ֱ������������ϣ�OΪԭ�㣬��A������Ϊ��6��0������B������Ϊ��0��8��������M�ӵ�O��������OA���յ�A��ÿ��1����λ���ٶ��˶���ͬʱ����N�ӵ�A��������AB���յ�B��ÿ�� ![]() ����λ���ٶ��˶�����һ�����㵽���յ�ʱ����һ������Ҳ��ֹ֮ͣ�˶����趯��M��N�˶���ʱ��Ϊt�루t��0����
����λ���ٶ��˶�����һ�����㵽���յ�ʱ����һ������Ҳ��ֹ֮ͣ�˶����趯��M��N�˶���ʱ��Ϊt�루t��0����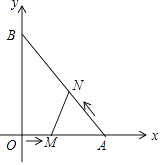
��1����t=3��ʱ��ֱ��д����N�����ꣻ
��2���ڴ��˶��Ĺ����У���MNA������Ƿ�������ֵ�������ڣ���������ֵ���������ڣ���˵�����ɣ�
��3����tΪ��ֵʱ����MNA��һ�����������Σ�
���𰸡�
��1��
�⣺��NC��OA��C��
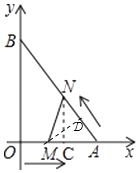
��t=3ʱ��AN=3�� ![]() =5��
=5��
��CN=ANsin��OAB=5�� ![]() =4��AC=ANcos��OAB=5��
=4��AC=ANcos��OAB=5�� ![]() =3��
=3��
��OC=OA��AC=3��
��N��3��4��
�ʴ�ΪN��3��4����
��2��
�⣺�����⣬AN= ![]() t��AM=OA��OM=6��t��
t��AM=OA��OM=6��t��
NC=NAsin��BAO= ![]() t
t ![]() =
= ![]() t��
t��
��S��MNA= ![]() AMNC=
AMNC= ![]() ����6��t����
����6��t���� ![]() t��
t��
=�� ![]() ��t��3��2+6��
��t��3��2+6��
���MNA����������ֵ�������ֵΪ6��
��3��
�⣺���ⷨ1��AM=6��t��AN= ![]() t ��0��t��6����
t ��0��t��6����
��AC=ANcos��BAO=t��
�ٵ�AM=ANʱ��6��t= ![]() t���� t=
t���� t= ![]() ��
��
�ڵ�MN=ANʱ����NC��ֱƽ���߶�MA��
��MC=AC=t
��OM+MC+CA=OA
��t+t+t=6 ���t=2
�۵�MN=MAʱ����DΪ�߶�AN���е㣬�� MD��ֱƽ���߶�AN
��AD= ![]() AN=
AN= ![]() ��
��
�֡�cos��DAM=cos��OAB ����ߡ�DAM�ס�OAB��
�� ![]() ��
�� ![]() ��� t=
��� t= ![]() ��
��
���ϣ���t��ֵȡ 2�� ![]() ��
�� ![]() ʱ����MAN�ǵ��������Σ�
ʱ����MAN�ǵ��������Σ�
���ⷨ2��AN= ![]() t��NC=
t��NC= ![]() t��AC=ANcos��BAO=t��
t��AC=ANcos��BAO=t��
��OC=OA��AC=6��t��
��MC=|OC��OM|=|6��t��t|=|6��2t|
Rt��NCM�� NM2=MC2+NC2
��NM= ![]() =
= ![]() ��
��
�� ![]() ��
��
�֣�AM=6��t��AN= ![]() t��0��t��6����
t��0��t��6����
�ٵ�MN=ANʱ��MN2=AN2
�� ![]() =
= ![]() ��
��
����t2��8t+12=0��t1=2��t2=6����ȥ����
�ڵ�MN=MAʱ��MN2=MA2
�� ![]() =��6��t��2��
=��6��t��2��
���� ![]() t2��12t=0��t1=0����ȥ����t2=
t2��12t=0��t1=0����ȥ����t2= ![]() ��
��
�۵�AM=ANʱ��6��t= ![]() t����t=
t����t= ![]() ��
��
���ϣ���t��ֵȡ 2�� ![]() ��
�� ![]() ʱ����MAN�ǵ��������Σ�
ʱ����MAN�ǵ��������Σ�
����������1����NC��OA��C����Rt��ANC�У����NC��AC���ɽ�����⣻��2������N��NC��OA��C�������⣬AN= ![]() t��AM=OA��OM=6��t��NC=NAsin��BAO=
t��AM=OA��OM=6��t��NC=NAsin��BAO= ![]() t
t ![]() =
= ![]() t����S��MNA=
t����S��MNA= ![]() AMNC=
AMNC= ![]() ����6��t����
����6��t���� ![]() t=��
t=�� ![]() ��t��3��2+6�����ݶ��κ��������ʼ��ɽ�����⣻��3�����������η����г����̼��ɽ�����⣮��
��t��3��2+6�����ݶ��κ��������ʼ��ɽ�����⣻��3�����������η����г����̼��ɽ�����⣮��