Question

【题目】发现问题：

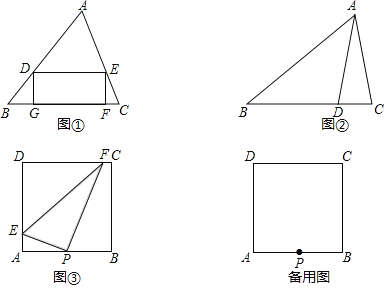
（1）如图①，四边形DEFG是△ABC的内接矩形，其中S△ABC＝15，BC＝6，DE＝4，则S四边形DEFG＝　 　；

探究问题：（2）如图②，在△ABC中，D是BC边上一点且BD＝AD＝AC＝10，∠BAD＝40°，请以点D为顶点作△ABC的内接三角形DEF（点E、F分别在AB、AC上），求其周长的最小值；

解决问题：（3）小红同学参加了物理课外兴趣小组．图③是其制作的一个光电感应装置在某时刻的平面情景图，在边长为20厘米的正方形ABCD中，P为AB的中点，点P位置是一个激光发射器，可以左右来回180°转动，同时在正方形ABCD内发出两条互相垂直的蓝色光线PE、PF，E、F是落在AD、DC、CB三边上的两个光点，E、F、P三点会在正方形ABCD内自动感应出一个发光△PEF，请问在激光器转动发射的过程中，形成的△PEF面积有无最大值，如果有，请求出；如果没有，请说明理由．

Answer 1

【答案】（1）；（2）30；（3）有，125cm2

【解析】

（1）如图①中，作AH⊥BC于H，交DE于T．利用相似三角形的性质求解即可．

（2）如图②中，作点D关于AB的对称点D′，作点D关于AC的对称点D″，连接D′D″交AB于E，交AC于F，连接DE，DF，此时△DEF的周长最小．证明△AD′D″是顶角为120°的等腰三角形即可解决问题．

（3）分三种情形：如图3中，当点E在线段AD上，点F在线段CD上时．如图④中，当点E在线段AD上，点F在线段BC上时．当点E在线段CD上，点F在线段BC上时，点E与点D重合时，分别求解即可解决问题．

（1）如图①中，作AH⊥BC于H，交DE于T．

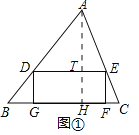
∵S△ABC＝BCAH＝15，BC＝6，

∴AH＝5，

∵四边形DEFG是矩形，

∴DE∥BC，

∴△ADE∽△ABC，

∴＝，

∴＝，

∴AT＝，

∴TH＝AH﹣AT＝5﹣＝，

∴矩形DEFG的面积＝DETH＝4×＝．

故答案为．

（2）如图②中，作点D关于AB的对称点D′，作点D关于AC的对称点D″，连接D′D″交AB于E，交AC于F，连接DE，DF，此时△DEF的周长最小．

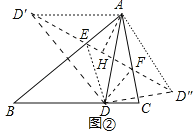
∵AD＝DB＝AC，

∴∠DAB＝∠B＝40°，

∴∠ADC＝∠C＝∠B+∠DAB＝80°，

∴∠DAC＝180°﹣80°﹣80°＝20°，

∴∠BAC＝∠BAD+∠DAC＝60°，

∵AD＝AD′＝AD″＝10，∠BAD＝∠BAD′，∠CAD＝∠CAD″，

∴∠D′AD″＝2∠BAC＝120°，

作AH⊥D′D″，

∵AD′＝AD″，

∴D′H＝HD″，∠D′AH＝∠D′AD″＝60°，

∴D′H＝AD′sin60°＝10×＝15，

∴D′D″＝2D′H＝30，

∵DE＝ED′，DF＝FD″，

∴△DEF的周长＝DE+EF+DF＝ED′+EF+FD″＝D′D″＝30，

∴△DEF的周长的最小值为30．

（3）如图3中，当点E在线段AD上，点F在线段CD上时，作FH⊥AB于H．则四边形BCFH是矩形，FH＝BC＝20cm．

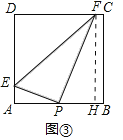
∵四边形ABCD是正方形，

∴AB＝BC＝20cm，

∵∠A＝∠EPF＝∠FHP＝90°，

∴∠APE+∠FPH＝90°，∠FPH+∠PFH＝90°，

∴∠APE＝∠PFH，

∴△APE∽△HFP，

∴＝＝＝，

∴PF＝2PE，

∴当PF的值最大时，△PEF的面积最大，

∴当点F与C重合时，△PEF的面积最大，此时PF＝＝10cm，PE＝5cm，

∴此时△PEF的面积的最大值为×5×10＝125（cm2）．

如图④中，当点E在线段AD上，点F在线段BC上时，延长EP交CB的延长线于H．

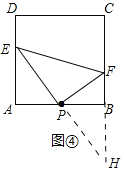
∵∠EAP＝∠PBH＝90°，∠APE＝∠BPH，AP＝PB，

∴△APE≌△BPH（ASA），

∴PE＝PH，

∵FP⊥EH，

∴FE＝FH，

∴S△EFP＝S△PFH＝FHPB＝5FH＝5EF，

∴EF的值最大时，△PEF的面积最大，

∴当点E与D重合或点F与点C重合时，△PEF的面积最大，最大面积＝125cm2，

当点E在线段CD上，点F在线段BC上时，点E与点D重合时，△PEF的面积最大，最大值为125cm2，

综上所述，△PEF的面积有最大值，最大值为125cm2．