题目内容
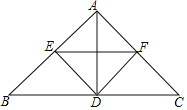
【题目】在平面直角坐标系中,O为坐标原点,点M、N位于第一象限,其中M的坐标为(m,5),点N的坐标(n,8),且m≥n.
(1)若MN与坐标轴平行,则MN= ;
(2)若m、n、t满足![]() ,MA⊥x轴,垂足为A,NB⊥x轴,垂足为B.
,MA⊥x轴,垂足为A,NB⊥x轴,垂足为B.
①求四边形MABN的面积;
②连接MN、OM、ON,若△MON的面积大于26而小于30,求m的取值范围.
【答案】(1)3;(2)①![]() ;
;![]()
![]() <m<
<m<![]()
【解析】
(1)由MN与坐标轴平行,且两点纵坐标不相等可得两点横坐标相等即:m=n,则两点间距离就是8-5=3;
(2)先将m、n用含t的代数式表示出来,就可以得到m与n之间的数量关系;
①根据题中描述可得四边形MABN为梯形,根据梯形的面积计算公式可算出结果;
②先把△MON面积的算法用含有m的代数式表示出来,再列出关于m的不等式组,解出即可
(1)∵M的坐标为(m,5),点N的坐标(n,8),
∴m=n,MN=8﹣5=3,
故答案为3;
(2)如图,∵m、n、t满足![]() ,
,
∴ ,
,
∴n=m﹣![]() ,
,
①∵MA⊥x轴,NB⊥x轴,
∴MA=5,NB=8,AB=m﹣n=m﹣(m﹣![]() )=
)=![]() ,
,
∴S梯形AMNB=![]() (MA+NB)MN=
(MA+NB)MN=![]() ×(5+8)×
×(5+8)×![]() =
=![]() ;
;
②由①知,S梯形AMNB=![]() ,MA=5,NB=8,
,MA=5,NB=8,
∵MA⊥x轴,NB⊥x轴,M(m,5),N(n,8),
∴OB=n,OA=m,
∴S△MON=S△OBN+S梯形AMNB﹣S△OAM=![]() n×8+
n×8+![]() ﹣
﹣![]() m×5=4n﹣
m×5=4n﹣![]() m+
m+![]() =4(m﹣
=4(m﹣![]() )﹣
)﹣![]()
![]() m+
m+![]() =
=![]() m+4,
m+4,
∵△MON的面积大于26而小于30,
∴26<![]() m+4<30,
m+4<30,
∴![]() <m<
<m<![]() .
.

练习册系列答案
 能考试期末冲刺卷系列答案
能考试期末冲刺卷系列答案
相关题目