题目内容
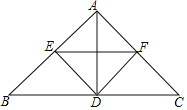
【题目】如图,在△ABC中,AB=AC,D是边BC上的一点,DE⊥AB,DF⊥AC,垂足分别是E、F,EF∥BC.
(1)求证:△BDE≌△CDF;
(2)若BC=2AD,求证:四边形AEDF是正方形.
【答案】(1)证明见解析;(2)证明见解析.
【解析】试题分析:
(1)用ASA证明△BDE≌△CDF;
(2)由BC=2AD,得∠BAC=90°,从而四边形AEDF是矩形,再由AE=AF即可得证.
试题解析:
证明:(1)∵AB=AC,∴∠B=∠C,
∵EF∥BC,∴∠AEF=∠B,∠AFE=∠C,∴∠AEF=∠AFE,
∴AE=AF,∴BE=CF,
∵DE⊥AB,DF⊥AC,∴∠AED=∠AFD=90°,
在△BED和△CFD中,
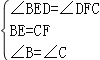 ,
,
∴△BDE≌△CDF.
(2)∵△BDE≌△CDF,∴BD=DC,DE=DF,
∵BC=2AD,∴AD=![]() BC,∴∠BAC=90°,
BC,∴∠BAC=90°,
∵DE⊥AB,DF⊥AC,∴∠EAF=∠AED=∠AFD=90°,∴四边形AEDF是矩形,
∵AE=AF,∴四边形AEDF是正方形.

练习册系列答案
 小学课堂作业系列答案
小学课堂作业系列答案 金博士一点全通系列答案
金博士一点全通系列答案
相关题目